Основная теорема зацепления

Синтез зубчатых механизмов

Основную теорему зацепления рассмотрим на примере двух зубчатых колес (рис. 26). Профили зубьев двух колёс, соприкасаются в точке К. Колёса вращаются вокруг точек 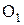и 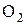в направлениях указанных стрелками. Скорость точки К в системе первого колеса:

(1.9)

Скорость точки К в системе второго колеса:

(1.10)

Они различны по величине и направлению.

Давление между двумя твёрдыми телами передаётся по общее нормали N-N, следовательно, непрерывная передача движения возможна только лишь в том случае, если проекции скоростей точек контакта обоих профилей на общую нормаль будут одинаковы по величине и направлению.

При 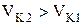будет происходить размыкание зацепления, чего допускать нельзя; при - происходит внедрение зуба одного колеса в зуб другого колеса другой (тем более нельзя допускать), следовательно, скорости должны быть равны

,

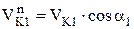
так как ,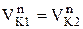

то

или учитывая (1.9) и (1.10) получим:

(1.11)

Из точек 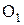и 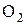опустим перпендикуляры и на общую нормаль N-N

;

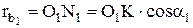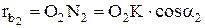
Рис. 1.26

следовательно, подставив в формулу (1.11) получим: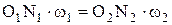

откуда

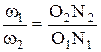
(1.12)

Соединим центры вращения профилей линей ; и точку пересечения с общей нормалью N-N обозначим Р.

Из подобия треугольников 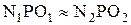следует: , учитывая формулу (1.12) получим:

(1.13)

Это равенство выражает основную теорему зацепления: общая нормаль N-N к сопряжённым профилям, вращающимся относительно центров 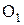и 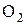, делит линию центров 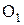и 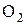на части обратно пропорциональные угловым скоростям этих профилей.

Итак: если точка Р неподвижна, то передаточное отношение звеньев будет постоянно. Точка Р называется полюсом зацепления. Она является мгновенным центром относительного вращения звеньев 1 и 2. Окружности с центрам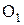и и 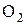проходящие через полюс называются начальными. При работе колёс катятся одна по другой без скольжения. Следовательно, как вытекает из формулы (1.13), они представляют собой центроиды колёс.

Угол 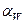, составленный общей нормалью N–N к профилям зубьев (линией зацепления) и общей касательной к начальным окружностям называется углом зацепления (углом давления).

По теореме зацепления всегда можно проверить, являются ли два профиля находящихся в зацеплении зубьев сопряженными. Для этого проводим к ним общую нормаль и выясняем, проходит ли она через полюс зацепления. Требование сопряжённости профилей удовлетворяется, если профили являются эвольвентными, циклоидными и в некоторых других случаях. В эвольвентном зацеплении угол постоянный. В большинстве случаев угол .

Образование эвольвенты и её свойства

Эвольвентой круга называют кривую, которая описывает любую точку прямой, перекатывающейся без скольжения по окружности. При этом прямую обычно называют производящей, а окружность - основной .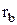

Пусть производящая прямая (рис. 1.27) n – n показана в положении, когда она касается основной окружности в точке А и требуется построить эвольвенту, описываемую т. М. Делим отрезок AM на равные части и откладываем на 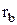дуги равные соответствующим частям отрезка AM: и так далее. Через полученные точки проводим касательные и откладываем на них отрезки, последовательно уменьшая длину каждого отрезка на одну часть. Соединяя концы отложенных отрезков, получаем эвольвенту. Уравнение эвольвенты получим из условия перекатывания производящей прямой по

(2.13)

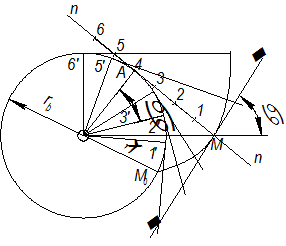
Рис. 1.27

Обозначим через 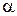острый угол между касательной к эвольвенте и радиус-вектором эвольвенты ОМ. Этот угол называется углом профиля. Угол, образованный начальным радиус-вектором эвольвенты и её текущим радиусом ОМ называется эвольвентным углом (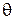). Тогда условие (1.14) принимает вид: или . Функция 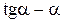называется инвалютой и обозначается "inv", то есть уравнение может быть записано 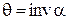. Радиус-вектор эвольвенты находится из треугольника ОАМ

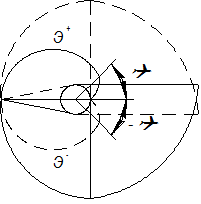
Эвольвента имеет две ветви (рис. 1.28): положительная ветвь получается при перекатывании прямой против хода часовой стрелки, отрицательная 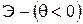- при перекатывании по ходу часовой стрелки.

Рис. 1.28

Дата добавления: 2014-01-20