Уравновешивание механизмов на фундаменте

Для уравновешивания плоского механизма на фундаменте необходимо и достаточно так подобрать массы звеньев этого механизма, чтобы общий центр масс движущихся звеньев его оставался неподвижным:

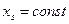
(4.9)

и центробежные моменты инерции масс звеньев относительно осей x и z, y и z были постоянными:

(4.10)

При соблюдении этих условий будут уравновешены главный вектор сил инерции и главные моменты сил инерции относительно осей x и y. Главный момент сил инерции относительно оси z, перпендикулярной к плоскости движения механизма, уравновешивается моментом движущих сил и сил сопротивлений на главном валу машины.

На практике при уравновешивании механизмов указанные условия (4.9) и (4.10) выполняются частично.

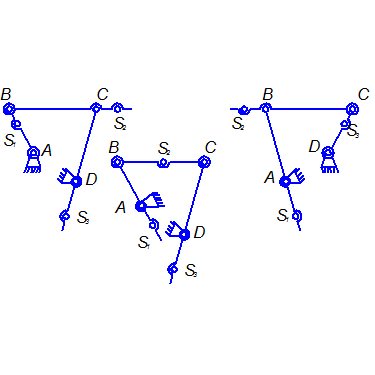
Рис. 4.3

Пусть, например, дан механизм шарнирного четырёхзвенника ABCD (рис. 4.3) требуется уравновесить только главный вектор сил инерции. Обозначим массы звеньев AB, BC и CD соответственно через и 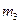; длины звеньев – через и 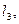а расстояние центров тяжести и 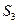этих звеньев от точек А, В и С – через 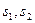и . Для удовлетворения условия (4.9.) необходимо, чтобы общий центр S масс механизма находился на прямой AD, либо между точками А и D, либо за ними. В этом случае центр S масс механизма при его движении будет оставаться неподвижным и, следовательно, главный вектор сил инерции механизма будет уравновешен.

Массы звеньев и положения центров тяжести их должны быть подобраны так, чтобы

		(4.11)
		(4.12)

Если механизм состоит из n подвижных звеньев, то при решение задач о подборе масс механизма, удовлетворяющих условию уравновешенности главного вектора сил инерции механизма, имеем 2n неизвестных величин; уравнений же, связывающих эти величины, можно составить (n-1). После произвольного выбора (n+1) величин остальные величины получают определённые значения. В исследуемом механизме количество подвижных звеньев n=3, количество подбираемых величин 2n=6, число же независимых уравнений n-1=2. Таким образом, задаваясь, например, значениями m₃ и s₃, из уравнения (4.12) получаем значение m₂s₂, в котором можно задаваться одним из неизвестных и получать другое. Подставляя полученные значения в уравнение (4.11), определяем значение m₁s₂, в котором также можно задаться одной величиной. Из уравнений (4.11) и (4.12) при различных исходных заданиях можно получить три варианта схем уравновешенного четырёхзвенного механизма Рис. 4.3(а, в, д). Следовательно, если считать, что расположение центра тяжести звена за его шарнирами соответствует как бы установке противовеса, то можно сказать, что задачу уравновешивания главного вектора сил инерции механизма шарнирного четырёхзвенника можно решить путём установки противовесов на двух его звеньях.

Аналогичным образом можно решить задачу подбора масс отдельных звеньев для уравновешивания шарнирного шестизвенника и любого механизма, образованного путём наслоения двухповодковых групп. Дав уравнения (9.) можно заменить одним векторным уравнением

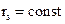
(4.13)

Где r_s - вектор, определяющий положение общего центра масс.

Условие (4.13) удовлетворяется в частности, когда r_s =0; это условие приводит к способу подбора механизмов с симметрично расположенными звеньями равных масс, вследствие чего получается самоуравновешивание механизма в целом.

Рис. 4.4

На рисунке 4.4 показаны схемы симметричных кривошипно-ползунного и шарнирного четырёхзвенного механизмов. В тех случаях, когда размещение звеньев в симметричных механизмах очень громоздко или подбор масс конструктивно нецелесообразен, применяется метод установки противовесов.

Пусть, например, требуется уравновесить только главный вектор сил инерции кривошипно-ползунного механизма, схема которого изображена на рисунке 4.5. Обозначим массы кривошипа 1, шатуна 2 и ползуна 3 через m₁, m₂, m₃ и будем считать их сосредоточенными соответственно в центрах тяжести S₁, S₂ и В звеньев. Устанавливаем на линии АВ в точке D противовес и определяем его массу m_пр из условия, чтобы центр тяжести масс m_пр, m₂ и m₃ совпадал с точкой А. Из уравнения статических моментов относительно точки А имеем

откуда

Массу 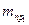, противовеса, установленного в точке С кривошипа, определяем из условия, чтобы центр тяжести масс 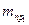, и 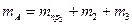совпадал с точкой О. Из уравнения статических моментов относительно точки О находим

Радиусы s и с противовесов выбираются произвольно. После установки противовесов центр масс механизма во всех его положениях будет совпадать с точкой О и, следовательно, будет во всё время работы оставаться неподвижным. Таким образом, два противовеса 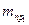и полностью уравновешивают все силы инерции рассматриваемого механизма. Однако подобное полное уравновешивание сил инерции кривошипно-ползунных механизмов на практике применяют редко, так как при малом значении радиуса с масса получается весьма большой, что ведёт к появлению добавочных нагрузок в кинематических парах и звеньях механизма. При большом значении радиуса с сильно увеличиваются габаритные размеры всего механизма. Поэтому, часто ограничиваются лишь приближённым уравновешиванием сил инерции. Так, в кривошипно-ползунных механизмах метод установки противовеса на кривошипе является наиболее распространённым методом приближённого уравновешивания сил инерции. В этих механизмах на практике часто применяют уравновешивание только массы кривошипа и части массы шатуна.

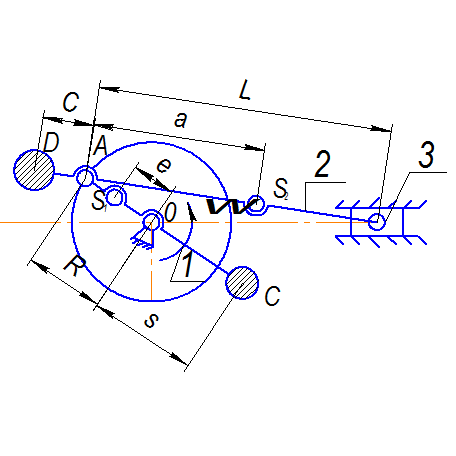
Рис. 4.5

Дата добавления: 2014-01-20