Коефіцієнт перекриття

Геометричні та кінематичні умови існування передачі

Профілі зубів, їх розташування відносно ділильного кола, розміри зубів за висотою та їх товщина на кожному зубчастому колесі, а отже, і властивості самої передачі, однозначно визначаються сукупністю значень трьох величин: коефіцієнтів зміщень x₁, x₂ і кута нахилу лінії зуба b. Вибір потрібних значень цих величин для конкретної зубчастої передачі (z₁, z₂, m) — один із перших і важливих етапів її проектування. Невдалий вибір цих параметрів (х₁, х₂,b) може призвести до погіршення кінематичних і міцністних характеристик передачі або навіть до неможливості перетворення руху за заданим законом.

Розглянемо явища, при яких неможлива реалізація запланованих кінематичних функцій передачі, і виведемо залежності, які описують їх. Ці залежності дозволяють сформулювати умови, які повинні задовольняти вибрані значення х₁ х₂ і b, щоб вказані явища були відсутні, тобто сформулювати умови існування передачі. До таких умов належать:

1) забезпечення плавності роботи зубчастої передачі;

2) усунення підрізання зубів;

3) усунення загострення зубів;

4) усунення інтерференції зубів.

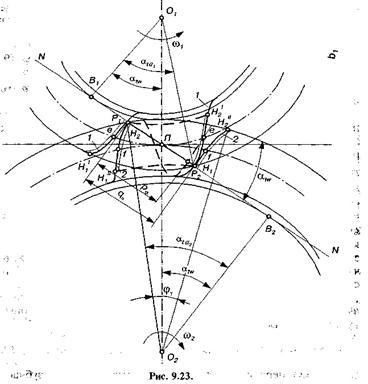Плавність роботи зубчастої передачі характеризується коефіцієнтом перекриття. Для його визначення розглянемо пару зубчастих коліс, які перебувають у зачепленні. Нехай зубчасті колеса обертаються так, як показано на рис. 9.23. Зуби при цьому будуть стикатися між собою по загальній нормалі NN, проведеній через точки контакту зубів. Причому зуби входять у контакт у точці H₂, а виходять з контакту у точці H₁. Ці два положення бічних профілів зубів зображено на рисунку: для шестірні — лініями 1, для колеса — лініями 2. Лінія NN називається лінією зачеплення. Частину цієї лінії між точками дотику В₁ і В₂ з основними колами, як уже відомо, називають теоретичною лінією зачеплення, а відрізок q_a= Н₁Н₂, що відсікається від лінії зачеплення колами виступів, активною лінією зачеплення. Активна лінія зачеплення є геометричним місцем точок контакту двох спряжених профілів. За межами лінії Н_{Н₂ контакт між зубами відсутній, оскільки він лежить за межами габаритів зубчастих коліс. Чим більша довжина активної лінії зачеплення відносно кроку евольвентного зачеплення р_а, тим вища плавність роботи передачі.

Під кроком евольвентного зачеплення розуміють відстань між двома контактними точками однойменних головних профілів двох сусідніх зубів. Оскільки однойменні профілі двох сусідніх зубів є еквідистантними кривими, відстань між якими визначається основним коловим кроком р_b, маємо

(9.63)

Точки Н_х і H₂ визначають також величину активного (робочого) профілю зубів. Оскільки за межами лінії Н_{Н₂ контакту між зубами коліс немає, точка Н₂ є найближчою до центра обертання О₁ точкою контакту профілю зуба шестірні, а найвідда-ленішою від центра O₁ є точка H₁. Отже, частина бічного профілю зуба шестірні є активною, у колеса активним є профіль 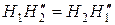(на рис. 9.23 активні профілі зубів позначені подвійними лініями). Характерно, що довжина активного профілю на головці зуба більша, ніж на спряженій ніжці зуба 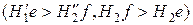. Нерівності ділянок профілів, які проходять контактні точки ніжки та головки зуба за однакові проміжки часу (у полюсі зачеплення П точки e і f збігаються), вказує на наявність відносного ковзання зубів, причому ніжка зуба перебуває у більш напруженому стані і більше спрацьовується.

Плавність робота зубчастої передачі характеризується повним коефіцієнтом перекриття, під яким розуміють відношення кута перекриття j_g, до кутового кроку t, тобто

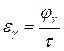(9.64)

де j_g — кут перекриття; t = 2p/z— центральний кут зубчастого колеса, що відповідає кроку зубчастого колеса.

Кутом перекриття називають кут повороту зубчастого колеса від положення входу зуба у зачеплення до його виходу із зачеплення.

Практично коефіцієнт перекриття показує число пар зубів, що перебувають одночасно у зачепленні.

Коефіцієнт перекриття повинен бути більшим від одиниці, інакше порушується плавність роботи передачі (співудари зубів, контакт кромками вершин). Чим вищий коефіцієнт перекриття, тим плавніше працює зубчаста передача, тим більша її несуча здатність. Внаслідок можливої неточності монтажу та спрацювання зубів коефіцієнт перекриття може виявитися меншим за розрахунковий, тому рекомендується вибирати мінімальним коефіцієнт перекриття e_g ³ 1,2.

Коефіцієнт перекриття &у можна також виразити як відношення дуги зачеплення до колового кроку.Зрозуміло, що для забезпечення плавної роботи передачі дуга зачеплення повинна бути більша від кроку.

Дугами зачеплення називають частину початкових кіл, які перекочуються одна по одній за час контакту пари зубів. Взагалі кажучи, дугу зачеплення і коловий крок можна знаходити на будь-якому іншому колі зубчастих коліс (вершин, ділильному, основному тощо).

Картину зачеплення у рейковому та внутрішньому зачепленнях зображено на рис. 9.24.

Торцевим коефіцієнтом перекриття називають відношення довжини активної лінії зачеплення до кроку евольвентного зачеплення.

Коефіцієнтом осьового перекриття називається відношення робочої ширини зубчастого вінця b_w до осьового кроку р_х (рис. 9 У прямозубій циліндричній передачі коефіцієнт e_b = 0, оскільки кут нахилу зубів b дорівнює нулю і в цьому випадку повний коефіцієнт перекриття дорівнює лише торцевому коефіцієнту перекриття (e_g = e_a).

Дата добавления: 2014-01-20