Основные понятия и определения. Кинематический анализ рычажных механизмов

Кинематический анализ рычажных механизмов.

Пространственные механизмы.

В пространственном механизме оси непараллельны, звенья могут двигаться в разных плоскостях.

W_пр= 6n - (S₁+ S₂+ S₃+ S₄+ S₅)

Допустим, что механизм, изображенный на рис.1.2.1 – пространственный и все кинематические пары 5-го класса, т.е. одноподвижны A_V,B_V,C_V,D_V, тогда

W_пр= 6n - (5p_V+4p_IV+3p_III+2p_II+p_I)

W_пр= 6^.3 - 5^.4 = -2 à статически неопределимая ферма.

Для получения W_действ=0, необходимо добавить 3 движения.

q= W_действ - W_пр = 1 - (-2) = 3,

где q – избыточные связи.

Для того чтобы их устранить, надо изменить класс некоторых кинематических пар, при этом нельзя изменять класс КП А. Поэтому, сделаем КП В – сферическим шарниром, т.е. 3-го класса (добавим 2 подвижности), а КП С – 4-го класса (добавим 1 подвижность). Тогда

W_пр= 6^.3 - (5^.2 + 4^.1 + 3^.1) = 18 - 17 = 1

_n

ФОРМУЛА СОМОВА-МАЛЫШЕВА: W_пр= 6^.n - ΣS_i + q

ⁱ⁼¹

Зависимость линейных координат в какой-либо точке механизма от обобщенной координаты – линейная функция положения данной точки в проекциях на соответствующие оси координат.

Х_с= f(j₁)

Зависимость угловой координаты какого-либо звена механизма от обобщенной координаты – угловая функция положения данного звена.

j₂= f(j₁)

Первая производная линейной функции положения точки по обобщенной координате – линейная передаточная функция данной точки в проекциях на соответствующие оси координат (иногда называют «аналог линейной скорости…»)

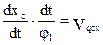
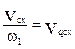
полная скорость т. С будет

Первая производная угловой функции положения звена по обобщенной координате – передаточное отношение.

Вторая производная линейной функции положения по обобщенной координате – аналог линейного ускорения точки в проекциях на соответствующие оси.

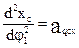
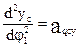
Вторая производная угловой функции положения звена по обобщенной координате – аналог углового ускорения звена.

Основными задачами кинематического исследования движения звеньев механизма явля­ются:

1) определение положения звеньев и траекторий заданных точек;

2) определение линейных и угловых скоростей и ускорений звеньев и отдельных точек механизма.

Для этой цели применяются следующие методы:

a) графический (планы скоростей и ускорений);

б) графоаналитический (метод диаграмм);

в) аналитический.

Методы а и б уступают в точности аналитическому, но обладают простотой и наглядностью.

Для выполнения анализа движения звеньев механизма должны быть за­даны:

а) схема механизма и

б) размеры его звеньев, а так же

в) функция зависимости перемещений ведущих звеньев от параметра времени или др. параметров их движения.

Построение планов механизма имеет целью определение относительных расположений звеньев и траекторий движения их точек по заданным поло­жениям ведущих звеньев. Решение этой задачи производится при помощи ме­тода засечек.

Планом механизма называют масштаб графического изображения кине­матической схемы соответствующей заданному положению входного звена.

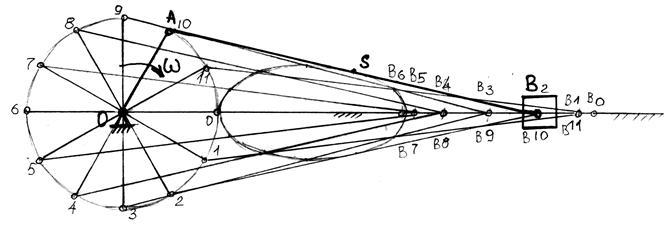Рис 1.

Определение скоростей и ускорений методом построения кинематичес­ких диаграмм.

Кинематической диаграммой принято называть зависимость какого-ли­бо параметра движения звена от времени или параметра перемещения веду­щего звена, представляемую графически кривой в прямоугольной системе координат.

Наивысший интерес представляют графики S, V, W ведомых звеньев. В качестве параметра S ведущего звена могут быть выбраны либо угол пово­рота, либо одна из координат принадлежащей ему точки. Эти параметры связаны с параметром времени.

Как известно, функции S,V и W движения какой-либо точки могут быть определены при помощи дифференцирования или интегрирования.

Дата добавления: 2014-01-20