Замена переменных в двойном интеграле. Пусть функции , взаимно однозначно отображают область (рис.7) в декартовых координатах

Пусть функции 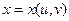, 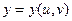взаимно однозначно отображают область 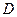(рис.7) в декартовых координатах 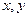на область 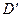(рис. 6) в криволинейных координатах .

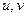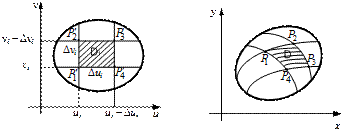
Рис. 6. Рис. 7.

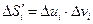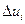В плоскости рассмотрим прямоугольную площадку, площадь которой (рис. 6). Ей соответствует криволинейный четырёхугольник (рис. 7) в плоскости . Если и 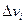достаточно малы, то криволинейный четырёхугольник 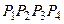можно считать параллелограммом. Его площадь можно вычислить как площадь параллелограмма, построенного на векторах 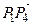и 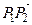. Для этого найдем координаты вершин .

Координаты точки : .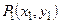

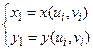Координаты точки 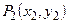определяются из системы:

,

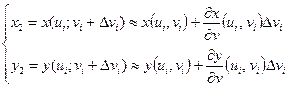в которой отброшены бесконечно малые более высокого порядка, чем .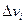

Координаты точки 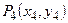определяются из системы

,

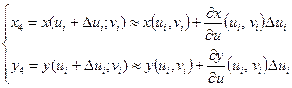в которой отброшены бесконечно малые более высокого порядка, чем .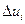

Площадь параллелограмма 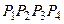определяется по формуле:

.

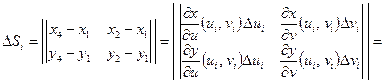
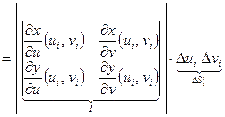Определитель - называется якобианом перехода от координат 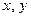к координатам 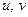. Через якобиан связаны площади элементарной области в координатах 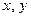и координатах .

.

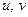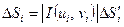Рассмотрим функцию 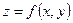- непрерывную в области 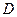. Тогда каждому значению функции 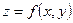в области 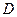соответствует то же самое значение функции в области 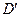, где .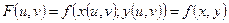

Интегральная сумма для функции 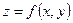в области 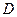будет иметь вид:

.

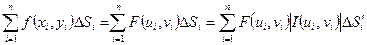Переходя в этой интегральной сумме к пределу при и при ранге дробления 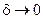, получим формулу преобразования координат в двойном интеграле:

.

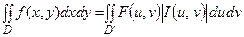Дата добавления: 2014-01-20