Физическая сторона задачи. Заключается в применении закона Гука

Заключается в применении закона Гука.

Закон Гука для угловых деформаций:

t = g×G (5), G – модуль сдвига (модуль упругости II–го рода)

G_стали = 8×10⁴ МПа = 8×10¹⁰ Па

Объединяя три стороны задачи, получаем:

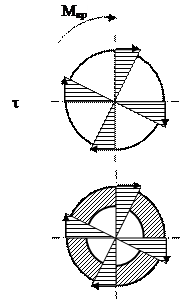
Рис. 8.3 Эпюра касательных напряжений

из (4), получаем g = r×q => (5) Mкр = 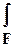t×r dF

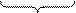
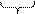t = r×s× G (6) => (2) M_кр = 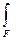r²×q×G dF (2) = q×G 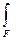r² dF

const I_p

I_p = 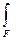r² dF – полярный момент инерции

I_x = I_y = p×D⁴/64; I_p = 2×I_x = 2×I_y = p×D⁴/32

q = M_кр/ (G×I_p) (7)

(7)®(6) => t = (M_кр×r×G)/I_p= (M_кр×r)/I_p

t = (M_кр×r_i)/I_p (8)

Анализируя формулу (8), делаем вывод, что касательные напряжения при кручении распределяются по нормальному закону (рис. 8.3).

t_max возникают при r =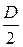

W_p = I_p/(D/2) – полярный момент сопротивления

Для круглого сплошного сечения: W_p = (p×D³)/16

Тогда t_max = M_кр/W_p; М_кр/W_к 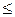[t], где W_к – момент сопротивления при кручении, равный в данный момент W_p.

t_max = M_кр/W_к£ [t] – условие прочности при кручении.

8.1.1 Геометрические характеристики I_p и W_p

характеристики	Ip	Wp
D
d D

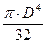
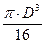
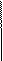
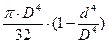
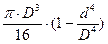
Анализируя эпюру t, мы видим, что в центре сечение не нагружено, т.о. рациональным сечением является не сплошной вал, а кольцо.

Задача

D₁

: сопоставить по металлоемкости два равноправных сечения (рис. 8.4).

Рис. 8.4 Полое и сплошное сечения вала

Равнопрочные:

t_max1 = t_max2

t_max1 = М_кр/W_p1

t_max2 = М_кр/W_p2

М_кр/W_p1 = М_кр/W_p1Þ 1/W_p1 = 1/W_p1

(p×D³₁)/16 = [(p×D³₂)/16]×(1–(d₂⁴/D₂⁴))Þ1/D₁³ = 1/(D₂³(1–0.8⁴));

0.59 D₂³ = D₁³;

D₁ = D×0.839.

Сопоставляем сечения 1 и 2 по металлоемкости:

F₁/F₂ = [(p×D₁²)/4]/[((p×D₂²)/4)–(1–d₂²/D²₂)] = 1.9.

8.2 Кручение прямоугольных стержней

При кручении прямоугольных стержней гипотеза плоских сечений не выполняется, так как сечения искривляются - депланируют. Задача о кручении прямоугольных стержней решается в теории упругости.

Готовые формулы

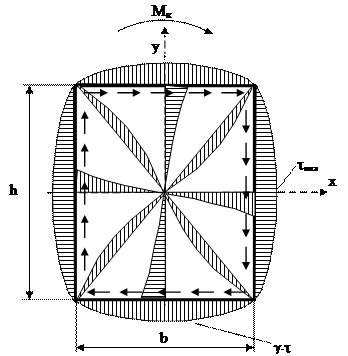h>b

Рис. 8.5 Эпюра касательных напряжений для некруглых стержней

В углах и центре тяжести 0

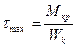
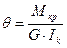
где W_k = a×b²×h - момент сопротивления при кручении

I_k = b×b³×h -

a, b, g -коэффициенты, зависят от соотношения

Дата добавления: 2014-01-20