Лекция 13. 5.3.1 Размеры зубчатых колес, формируемые при нарезании

5.3.1 Размеры зубчатых колес, формируемые при нарезании

стандартным инструментом реечного типа

Зависимости для определения основных геометрических размеров можно разделить на две категории:

- размеры колес, формируемые при нарезании (в данном коротком курсе рассматривается только нарезание эвольвентных колес методом обката инструментом реечного типа). Вывод соответствующих формул для определения этих размеров производится из рассмотрения зацепления нарезаемого колеса с производящим исходным контуром (рисунок 41). К ним относятся – диаметр основной окружности (которая определяет форму эвольвенты), диаметр окружности впадин, толщина зуба на делительной окружности и на окружности произвольного радиуса, шаг на основной окружности, положение граничной точки l на профиле зуба (точка, в которой начинается переходная кривая, плавно сопрягающая эвольвенту с окружностью впадин – рисунок 44).

В связи с ограниченным объемом времени на изучение курса ниже приводятся формулы для определения указанных размеров без изложения соответствующих выводов:

- диаметр делительной окружности

d= m^.Z

- диаметр основной окружности

d_b=m^.Z^.cosa;

- диаметр окружности впадин

d_f=m^.(Z – 2^.ha*-2^.c*+2^.x);

- толщина зуба на делительной окружности колеса

;

- толщина зуба на окружности произвольного радиуса

,

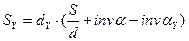здесь эвольвентный угол inva_Y определяется через функцию косинуса

;

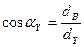- шаг на делительной окружности

p=p ^. m;

- шаг на основной окружности

p_b=p^. m^.cosa;

- угол профиля в граничной точке l

.

2) размеры, характеризующие зацепление пары колес. Эти размеры определяются из рассмотрения картины зацепления рассматриваемой пары (рисунок 39). К ним относятся – межосевое расстояние, угол зацепления, диаметры начальных окружностей, положение нижних точек рабочих участков профилей зубьев. Особое место занимает расчет диаметров вершин. Диаметр вершин – это диаметр заготовки, на которой нарезаются зубья. В принципе он может быть назначен конструктором произвольно. Однако существуют различные системы расчета диаметров вершин. Наиболее часто применяется система расчета, при которой обеспечивается сохранение стандартного радиального зазора в зацеплении колес. В этом случае диаметр вершин одного колеса зависит от межосевого расстояния и диаметра впадин сопряженного колеса. Поэтому данный параметр также относят к геометрии пары колес. Ниже, также без выводов, приводятся соответствующие формулы геометрического расчета:

- угол зацепления (определяется через эвольвентный угол inva_w)

,

(inva_w=tga_w-a_w) a_w;

- межосевое расстояние

Формулы для определения угла зацепления a_w и межосевого расстояния a_w выводятся из условия плотного беззазорного зацепления (боковой зазор в зацеплении колес отсутствует). Как видно из полученных формул их величины зависят от суммарного коэффициента смещения (x_S=x₁+x₂). Таким образом, изменяя суммарный коэффициент смещения, можно целенаправленно менять межосевое расстояние. В зависимости от величины суммарного коэффициента смещения различают следующие виды передач:

1) x_S=x₁+x₂=0 – равносмещенная передача (x₁= - x₂), в частном случае нулевая передача (x₁=x₂=0). У равносмещенных и нулевых передач угол зацепления равен углу профиля исходного контура (a_w=a= 20⁰); межосевое расстояние равно делительному межосевому расстоянию

;

диаметры начальных окружностей совпадают с диаметрами делительных окружностей (d_W1=d₁, d_W2=d₂);

2) x_S=x₁+x₂>0 – положительная передача (a_w>a, a_w>a);

3) x_S=x₁+x₂<0 – отрицательная передача (a_w<a, a_w<a).

- диаметры начальных окружностей

d_w1=2^.a_w/(u+1), d_w2=u^.d_w1,

где

u=Z₂/Z₁ – передаточное число (не надо путать с передаточным отношением: передаточное отношение – это кинематическая характеристика, оно может быть больше или меньше единицы, может быть положительным и отрицательным числом; передаточное число – это геометрическая характеристика – отношение числа зубьев большего колеса пары к числу зубьев меньшего колеса, оно всегда положительное и всегда больше единицы);

- диаметры окружностей вершин

d_a1=2^.a_w–d_f2–2^.c* ^. m,

d_a2=2^.a_w–d_f1–2^.c* ^. m.

5.3.2 Геометрические показатели качества зацепления

При проектировании зубчатой передачи необходимо проверить геометрические показатели, которые могут привести к неудовлетворительной ее работе.

К ним относятся:

- коэффициент перекрытия. Коэффициентом перекрытия называется отношение дуги зацепления к шагу зацепления на той же окружности (дуга зацепления – это путь, проходимый точкой зуба по дуге окружности за время работы данной пары – на рисунке 39 б показана дуга зацепления по основной окружности – b₁b₂). Если дуга зацепления окажется меньше шага, то при выходе из зацепления одной пары зубьев следующая не вступит в зацепление. Нарушается преемственность в работе пар, передача работает с ударами и быстро выходит из строя. Поэтому коэффициент перекрытия должен быть больше или, в крайнем случае, равен единице. Чем больше коэффициент перекрытия, тем более плавной будет работа передачи. На основании третьего свойства эвольвенты рабочая часть линии зацепления Р₁Р₂ равна дуге зацепления на основной окружности (рисунок 39 б), а расстояние между работающими профилями двух соседних зубьев, измеренное по линии зацепления равно основному шагу. Поэтому коэффициент перекрытия можно вычислить как отношение отрезка Р₁Р₂ к основному шагу р_В (рисунок 43):

.

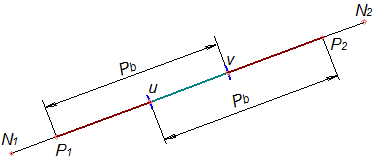
Рисунок 43

После преобразований получаем:

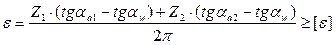
В этой формуле a_a1 и a_a2 – углы профиля на окружности вершин первого и второго колеса соответственно. Определяются через функцию косинуса:

, .

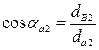Рекомендуется принимать следующие значения допускаемого коэффициента перекрытия:

[e]=1,05…1,1 – для неответственных передач,

[e]=1,2 – для ответственных передач.

При нарезании колес стандартным инструментом реечного типа коэффициент перекрытия в цилиндрической передаче не может превышать значения 1,88. То есть в реальных передачах значения коэффициента перекрытия располагаются в интервале 1,05…1.8. Это означает, что какую-то часть времени работают две пары зубьев одновременно, какую-то – одна пара зубьев. В тот момент времени, когда пара зубьев входит в зацепление в точке Р₁, предыдущая пара находится от нее на расстоянии основного шага в точке “ v ” линии зацепления (рисунок 43). С этого момента в зацеплении находятся две пары (и делят передаваемую нагрузку между собой). Когда предыдущая пара подойдет к точке Р₂, то следующая пара будет располагаться в точке" u ” (на расстоянии основного шага от точки Р₂). В следующий момент предыдущая пара выйдет из зацепления, а следующая войдет в зону ” uv ” и будет воспринимать всю нагрузку целиком. Пока пара находится в зоне“ uv ”никакая другая пара находиться в зацеплении не будет. Поэтому эта часть линии зацепления называется зоной однопарного зацепления. Часть профиля, которая работает в зоне однопарного зацепления, является наиболее напряженной частью этого профиля. Чем больше коэффициент перекрытия, тем меньше зона однопарного зацепления, тем большую часть времени в зацеплении находятся две пары зубьев.

- интерференция зубьев зубчатых колес. Профиль зуба состоит из двух характерных частей – из эвольвентной части, и переходной кривой, плавно сопрягающей эвольвентную часть с окружностью впадин (рисунок 44 а).

а) б) в)

Рисунок 44

Если рабочая часть профиля располагается целиком на его эвольвентной части, то происходит нормальная работа зубьев без нарушения основного закона зацепления (рисунок 44 б). Если же нижняя точка Р рабочего участка окажется ближе к основной окружности, чем граничная точка l сопряжения эвольвенты с переходной кривой, то вершина зуба одного колеса будет стремиться к внедрению в переходную кривую второго (рисунок 44 в). Вершина зуба одного колеса накладывается (на чертеже) на переходную кривую второго (как отмечалось выше, это явление называется интерференцией профилей). Нарушается основной закон зацепления, происходит заклинивание или поломка передачи. Интерференция отсутствует, если нижняя точка рабочего участка профиля зуба Р располагается на профиле выше граничной точки l. Положение точки на эвольвенте можно задать через различные параметры (через диаметр, через угол профиля, через угол развернутости, через эвольвентный угол). Наиболее удобные формулы получаются через углы профиля в рассматриваемых точках (формула для определения угла профиля в граничной точке l приведена выше, формулы для определения угла профиля в точках Р₁ и Р₂ получаются из рассмотрения рисунка 39 б):

,.

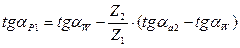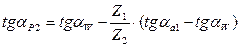Условие отсутствия интерференции:

- на ножке зуба первого колеса

tga_P1 > tga_l1;

- на ножке зуба второго колеса

tga_P1 > tga_l1;

- заострение зубьев. Если расчетный диаметр вершин окажется больше диаметра окружности, на которой происходит пересечение встречных эвольвент, формирующих зуб, то фактический диметр вершин окажется меньше расчетного (значит уменьшится коэффициент перекрытия), а зуб будет иметь острую вершину (рисунок 45 а).

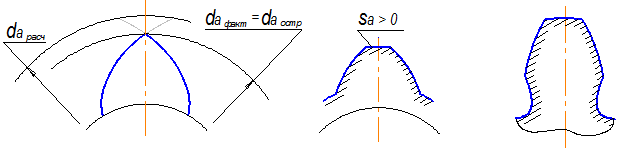
а) б) в)

Рисунок 45

При приложении нагрузки к вершине будут возникать большие напряжения (теоретически площадь равна нулю), что приведет к смятию пластичного материала или к разрушению хрупкого материала у этой вершины. Поэтому при проектировании передачи необходимо обеспечить у зуба некоторую толщину на окружности вершин S_a>0 (рисунок 45 б). При проверке на отсутствие заострения толщина зуба на окружности вершин сравнивается с допускаемой величиной:

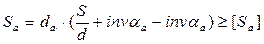
Рекомендуется принимать следующие значения допускаемой толщины зуба на окружности вершин:

[S_a]=0,25^.m – для пластичных материалов;

[S_a]=0,40^.m – для хрупких материалов;

- подрезание (подрез) зубьев. При определенных условиях инструмент начинает пересекать им же сформированную эвольвенту у основания зуба. Формируемая им переходная кривая в этом случае пересекает эвольвенту изнутри (а не плавно с ней сопрягается), а зуб становится более тонким (ослабленным) у основания. Это явление носит название подрезания или подреза зубьев (рисунок 45 в).

Зубья с подрезом можно применять для несиловых передач, если оставшийся участок эвольвенты обеспечивает необходимый коэффициент перекрытия. Для силовых передач применять зубья с подрезом не рекомендуется. При применении стандартного инструмента реечного типа подрез зубьев происходит в том случае, когда верхняя точка прямолинейного участка профиля зуба рейки заходит за точку N линии зацепления (рисунок 41). Поэтому проверка на отсутствие очень простая:

tga_l > 0.

Вероятность подреза повышается с уменьшением числа зубьев колеса. Если изготавливать колеса стандартным инструментом реечного типа без применения смещения, то подрез будет наблюдаться у колес с числом зубьев меньше 17 (Z_min=17), и чем меньше число зубьев, тем более значительным будет подрез. Однако, если правильно подобрать коэффициент смещения, то колесо с любым число зубьев можно нарезать без подреза. Подрез у колеса с заданным числом зубьев будет отсутствовать, если коэффициент смещения будет не меньше минимального:

.

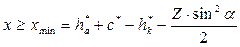Влиять на все указанные геометрические показатели качества зацепления можно правильным выбором коэффициентов смещения. Для рационального выбора коэффициентов смещения при проектировании передачи разработаны так называемые блокирующие контуры. Так как показатели описываются соответствующими математическими зависимостями, то их можно представить в виде линий в определенной системе координат. Совокупность этих линий в системе координат (x₁ – x₂ ) для определенной пары колес (z₁ – z₂) представляет собой замкнутый контур, отделяющий разрешенную зону для выбора коэффициентов смещения (x₁ и x₂) от запрещенной. Этот замкнутый контур и называется блокирующим контуром. Он позволяет конструктору спроектировать бесчисленное количество работоспособных передач с одинаковыми числами зубьев колес, но с различными свойствами.

Дата добавления: 2014-01-20