Выражение ошибки численного решения через изменения коэффициентов дифференциального уравнения

Сравнивая точное решение (5) с приближенным численным решением (7) можно видеть, что процедура вычисления на шаге h для них одинакова: предыдущее значение X(t) умножается слева на некоторую матрицу. Однако в точном решении X(t) умножается на матрицу полной экспоненты eAh, а в приближенном - на матрицу усеченной экспоненты е Ah.

Зададимся вопросом: для какого, измененного по отношению к (1), уравнения приближенное численное решение X (t+h) из(7) является точным?

Измененное уравнение (1) запишем следующим образом:

(2.1.10)

Его точное решение на шаге h

X(t+h) = e(A+dA)hX(t) (2.1.11)

Приравняв выражения (2) и (11), можно получить:

e(A+dA)h= e Ah (2.1.12)

Это уравнение определяет матрицу dA из уравнения (10).

Матричную экспоненту (12) представим в виде:

e(A+dA)h= eAhedAh

Отсюда и из (6) можно получить:

edAh– I = - e-Ah de Ah (2.1.13)

Представив матрицы в виде степенных разложений и оставляя только главные члены, получим приближенное соотношение:

dAh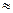- (Ah)r+1/(r+1)! (2.1.14)

Соотношения (13) и (14) позволяют вычислить матрицу dA, входящую в измененное уравнение (10). Точное решение этого уравнения совпадает с приближенным численным решением уравнения (1) методом r-того порядка. Таким образом, матрицу dA можно использовать в качестве характеристики погрешностей численного решения через изменение коэффициентов дифференциального уравнения (1).

Используя (14) можно выразить локальную ошибку численного решения (9) через dA:

dX (t+h) = - dAhX(t)

Если по условиям решаемой задачи можно сформулировать допустимые изменения коэффициентов dA, то соотношения (13) и (14) позволят осуществить предварительный выбор порядка метода r и шага дискретизации h.

Дата добавления: 2014-01-20