Повышение точности численного решения методом коррекции уравнений движения

Приближенное численное решение X(t+h) = e AhX(t) дифференциального уравнения (1) эквивалентно точному решению Х(t+h) = e(A+dA)hX(t) измененного уравнения

,

где dA определяется из соотношения

eAh= e(A+dA)h

Это позволяет поставить задачу о предварительной коррекции исходного уравнения таким образом, чтобы численное решение скорректированного уравнения стало равным точному решению исходного уравнения. Исходное уравнение (1) имеет точное решение на шаге:

X(t+h) = eAhX(t) (2.1.29)

Введем скорректированное уравнение

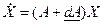(2.1.30)

Численное решение уравнения (30) на шаге можно записать так:

X (t+h) = e (A+ dA)hX(t) (2.1.31)

Здесь

e (A+ dA)h= [I + (A+ dA)h + …(A+ dA)rhr/r! ] (2.1.32)

- усеченная экспонента матрицы (A+ dA).

Приравнивая решения (29) и (31), можно получить соотношения:

eAh= e (A+ dA)h; e (A+ dA)h– e Ah= de Ah (2.1.33)

Отсюда, используя соотношения (6) и (32)и пренебрегая старшими степенями dA, получим:

dA h [I + Ah + …+ (Ah)(r-1)/(r-1)! ] = de Ah (2.1.34)

В первом приближении оценку dA получим из (5.34) с учетом (6):

dA h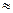(Ah)(r+1)/(r+1)! (2.1.35)

Сравнивая (35) с (14) можно видеть, что в первом приближении

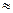dA -dA

Уравнения (5.33)…(5.35) с разной степенью точности определяют корректирующую матрицу dA, которую нужно прибавить к матрице исходного уравнения (5.1), чтобы численное решение скорректированного уравнения (5.30) совпало с точным решением на шаге исходного уравнения (1). Диагонализируя соотношения (33)…(35), получим:

eLh= e (L+ dL)h; e (L+ dL)h– e Lh= de Lh

dL h [I + Lh + …+ (Lh)(r-1)/(r-1)! ] = de Lh (2.1.36)

dL h = (Lh)(r+1)/(r+1)!

Все выражения в (36) являются диагональными матрицами, поэтому могут быть переписаны в скалярном виде:

eZkh= e (Zk+ dZk)h; e (Zk+ dZk)h– e Zkh= de Zkh

dZk h [I + Zkh + …+ (Zkh)(r-1)/(r-1)! ] = de Zkh (2.1.37)

dZk h = (Zkh)(r+1)/(r+1)! k= 1…n

Уравнения (37) с разной степенью точности определяют

приращения dZk, на которые нужно скорректировать

собственные значений Zkматрицы А, чтобы численное решение измененного таким образом уравнения совпало с точным решением на шаге исходного уравнения (1).

Приведенные в разделе 2.1 результаты получены для решения линейных однородных дифференциальных уравнений методом разложения в ряд Тейлора. Однако, во многоих случаях, полученные оценки могут быть распростронены на:

- неоднородные уравнения [2.5]

- линеаризуемые уравнения

- другие одношаговые методы решения дифференциальных уравнений, основанные на приближении локальной ошибки к ошибке разложения в ряд Тейлора.

Дата добавления: 2014-01-20