Достаточные условия потенциальности

Теорема. Если область V и поле 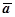(M) удовлетворяют следующим условиям:

1. V - односвязная область;

2. Поле 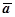(M) - безвихрево (т.е. ),,

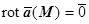то 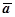(M) - потенциальное в V поле.

Доказательство. Напомним определение односвязной области: область (на плоскости, в пространстве) называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области. Нам при доказательстве теоремы придётся строить поверхности, натянутые на контуры; определение односвязности как раз гарантирует, что такие поверхности существуют, и ими могут служить поверхности, образующиеся при деформации контура в точку.

1. Докажем, что если выполняются условия теоремы, то линейный интеграл поля 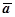(M) по любой кривой , целиком лежащей в V, определяется только начальной и конечной точками этой кривой, и не зависит от её формы. Пусть ASB и ATB - два пути, соединяющие точки А и В. Вместе они образуют замкнутый контур ASBTA. Пусть - кусочно-гладкая поверхность, натянутая на этот контур. Тогда по формуле Стокса , так как 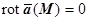. Но .

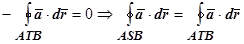2. Докажем, что если мы фиксируем точку и возьмём , то , т.е. определённая таким образом функция 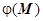действительно является потенциалом поля 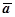(M). Это доказательство полностью повторяет доказательство теоремы пункта 16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути. Именно, требуется доказать, что 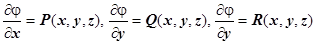. Действительно, пусть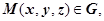

. Тогда ,

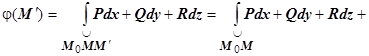
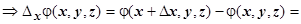
(на ) 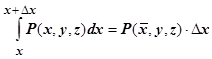(по теореме о среднем) 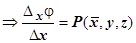. Точка удовлетворяет условиям 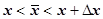. Устремим , тогда , и .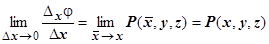

Аналогично доказывается, что .

18.1.4. Нахождение потенциала. В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля (M), то , где - фиксированная точка. Обычно, если в точке О (0,0,0) поле не имеет особенностей, то в качестве точки берётся именно эта точка; если в этой точке поле не определено, берётся другая точка. Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим .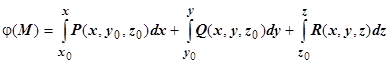

Пример. Доказать, что поле потенциально, и найти потенциал этого поля.

Решение. Мы будем доказывать, что это поле потенциально в любой односвязной области V, не содержащей точку О (0,0,0). Условие безвихревости поля :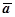

в координатной форме сводится к равенствам , , 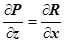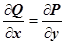. В нашем поле , ,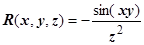. Находим производные:

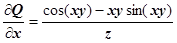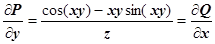, ; , ; , . Потенциальность поля доказана.

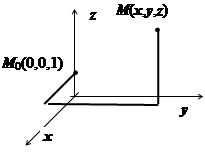
Ищем потенциал. Интеграл вычисляем по изображённому на рисунке пути, отправляясь от точки М ₀(0,0,1). 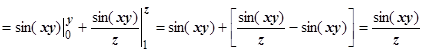. Если бы мы взяли в качестве точки М ₀ другую точку М ₁, то получили бы выражение, отличающееся на некоторую постоянную (более точно, на 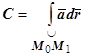); поэтому .

Дата добавления: 2014-01-20