Лекция № 8. Планетарные и волновые передачи

Тема 2. МЕХАНИЧЕСКИЕ передачи

Вопросы, изложенные в лекции:

8. Планетарные передачи.

9. Волновые передачи.

Планетарные передачи.

Рис. 8.1. Планетарная передача (редуктор).

В предыдущих лекциях речь шла о зубчатых передачах с неизменяемой геометрией звеньев. В этих механизмах положение зубчатых колёс и их конфигурация в процессе работы передачи оставались неизменными. Однако в многоцелевых самодвижущихся машинах, и особенно в машинах войскового применения, находят всё более широкое использование передачи с изменяемой геометрией формы или расположения подвижных звеньев. Наиболее широко из передач такого вида используются планетарные и волновые передачи.

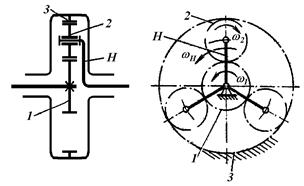Рис. 8.2. Планетарная передача (кинема­тическая схема): 1 –солнечное колесо; 2 – сателлит; 3 –эпицикл; H – водило.

Планетарной называется передача, имеющая в своём составе зубчатые колёса с перемещающимися геометрическими осями (рис. 8.1). Такие колёса (рис. 8.1, поз. 2) принято называть сателлитами. Колёса, геометрические оси которых совпадают с общей осью передачи (с осью входного и выходного валов), называют центральными. Центральное колесо с зубьями на внешней стороне обода (рис. 8.1, поз. 1), то есть направленными от оси вращения колеса, называют солнечной шестерней, а второе центральное колесо, взаимодействующее с сателлитами внутренними зубьями (рис. 8.1, поз. 3), то есть направленными к оси колеса, называют эпициклическим или просто эпициклом. Звено, несущее на себе подвижные оси сателлитов, называют водилом (рис. 8.1, поз. 4). На кинематических схемах (рис. 8.2) зубчатые колёса обычно обозначают арабскими цифрами, а водило – буквой H или h.

Простейшая планетарная передача обычно включает одно солнечное колесо, один эпицикл и одно водило. Такую планетарную передачу принято называть простым планетарным рядом. Главной кинематической характеристикой простого планетарного ряда является его кратность [4]; где z₃ – количество зубьев эпицикла; а z₁ – количество зубьев солнечного колеса. По количеству планетарных рядов планетарные передачи бывают одно-, двух-, трёх-, четырех- и многорядные. В российской литературе часто используют классификацию планетарных передач, предложенную проф. В.Н. Кудрявцевым. По этой классификации число центральных колёс обозначается цифрой и буквой K, далее в обозначении передачи через тире указывается число водил, равное количеству планетарных рядов, и буква H. Согласно этой классификации представленная на рис. 8.2 кинематическая схема будет соответствовать передаче 2К-Н.

Планетарный ряд, у которого ни одно из звеньев не соединено со стойкой, обладает двумя степенями свободы, то есть требует для однозначного характера движения всех своих звеньев подвода движения извне к двум из этих звеньев. Такой механизм принято называть дифференциальным. Если же в планетарном дифференциальном механизме одно из звеньев соединить со стойкой (сообщить ему постоянную скорость вращательного движения равную 0 радиан в секунду), то такой механизм превращается в передачу. Связывание со стойкой (или между собой) разных звеньев дифференциального планетарного ряда ведёт к изменению передаточного числа планетарной передачи. Применив этот приём к простому планетарному ряду, можно получить, по крайней мере, 7 вариантов передачи с различными передаточными отношениями**, представленными в таблице 8.1.

Таблица 8.1.Варианты передаточных отношений простого планетарного ряда (рис. 8.2)

№ п/п	№ входного звена	№ выходного звена	№ заторможенного звена	Передаточное отношение i
1	1	3	H	-K
2	1	H	3	1+K
3	3	1	H	-K^-1
4	3	H	1	1+K^-1
5	H	1	3	(1+K)^-1
6	H	3	1	(1+K^-1)^-1
7	1	H	-	1

Примечание: Вариант 7 соответствует непосредственному соединению входного и выходного звеньев механизма.

Данные таблицы 8.1 показывают, что использование простого планетарного ряда в качестве коробки передач транспортного средства позволяет получить 5 различных скоростей вперёд и 2 – назад при кратности изменения скоростей: вперёд , назад .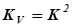

Такие возможности планетарного ряда предопределили его использование как в качестве самостоятельных передач (бортовой редуктор БМП-2 и танков Т72), так и в коробках передач (БМП-3, танки Т80, Т90). Применение планетарных механизмов в коробках передач обеспечивает следующие преимущества:

1. уменьшение габаритов трансмиссии;

2. высокую надежность работы (сохранение работоспособности даже при потере нескольких зубьев на центральных колёсах);

3. высокий КПД при относительно больших передаточных числах;

4. отсутствие поперечной нагрузки на основных валах;

5. возможность изменения передаточного числа без вывода зубчатых колёс из зацепления;

6. возможность отсоединения вала двигателя от трансмиссии при использовании фрикционов коробки передач (коробка передач одновременно выполняет роль главного фрикциона);

7. высокую скорость переключения передач, что способствует повышению среднего темпа движения машины.

недостатки планетарных передач:

1. необходимость повышенной точности изготовления вследствие наличия избыточных связей (наличия «лишних» сателлитов);

2. резкое снижение КПД при больших передаточных числах.

Как правило, планетарные передачи, имеющие в своём составе эпициклические колёса, отличаются более высоким КПД по сравнению с передачами, состоящими только из колёс внешнего зацепления. Именно поэтому в планетарных коробках передач используются простейшие планетарные ряды с эпициклом. Число переключений в одном ряду обычно не превосходит трёх с целью упрощения системы управления фрикционами и тормозами. Количество планетарных рядов в одной коробке передач тоже обычно не бывает более трёх.

Особенности проектирования и расчёта планетарных передач связаны с наличием избыточных кинематических связей (нескольких сателлитов). Предельно возможное число сателлитов в одном планетарном ряду ограничивается условием соседства, которое гласит: число сателлитов в планетарном ряду должно быть таким, чтобы соседние сателлиты не касались друг друга. Анализ геометрии планетарного ряда позволяет записать для возможного числа сателлитов ограничение сверху:

при расчёте по солнечному колесу (внешнее зацепление) -	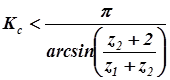;	(8.1)
при расчёте по эпициклу (внутреннее зацепление) -	;	(8.2)

где z₁, z₂, z₃ – числа зубьев солнечного колеса, сателлита и эпицикла, соответственно, а углы выражены в радианной мере. Но в практике машиностроения число сателлитов редко принимают более шести в связи с трудностью обеспечения равномерного распределения нагрузки между ними при большом их количестве.

Второе необходимое условие существования планетарного ряда называется условием соосности. Суть его вытекает из необходимости соблю­дения соосности центральных колёс, солнечного и эпицикла, и водила. Для простого планетарного ряда это условие выливается в равенство межосевых расстояний зацепления солнечного колеса с сателлитом a_1-2 и зацепления са­теллита с эпициклом a_2-3. Так как в планетарных рядах применяются пре­имущественно прямозубые колёса, а в простом ряду все колёса одного мо­дуля m, можем записать

. (8.3)

Приравнивая друг другу правые части равенств (8.3), получаем

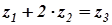; (8.4)

после деления обеих частей равенства на z₁ имеем

; (8.5)

что для передаточного числа между солнечным колесом и сателлитом даёт

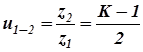. (8.6)

Но, как известно, передаточное число простого планетарного ряда максимально при ведущем солнечном колесе и ведомом водиле

; (8.7)

и для такой кинематической схемы имеем

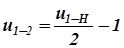. (8.8)

Третье условие диктуется необходимостью равномерного размещения сателлитов по окружности вокруг солнечного колеса и называется условием сборки. В конечном итоге это условие выливается в следующее требование: отношение чисел зубьев центральных зубчатых колёс к числу сателлитов должно быть целым числом или в формульном выражени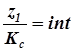и

и 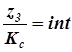; (8.9)

где int (читается «интегер») – аббревиатура, означающая любое целое число.

разветвление потока мощность при передаче силовых нагрузок через сателлиты обусловливает необходимость принятия специальных мер для обеспечения равномерности распределения нагрузок между сателлитами. Причин неравномерной загрузки сателлитов может быть несколько: неточность изготовления зубчатых колёс, неодинаковость межосевого расстояния у разных сателлитов, перекос геометрических осей сателлитов (непараллельность осей сателлитов и главной оси передачи) и др. При необеспечении равномерного распределения нагрузки между сателлитами расхождение между её величиной у отдельных сателлитов может достигать до 70 %.

Выравнивание нагрузки между сателлитами может быть достигнуто путём:

1. повышения точности изготовления всех деталей передачи;

2. выполнения одного из центральных колёс или водила плавающим, то есть имеющим некоторую радиальную подвижность относительно корпуса и сопряжённых деталей (эпицикл в бортовом редукторе БРДМ), и

3. использование упругих элементов конструкции (обод эпицикла повышенной гибкости, оси сателлитов малой жёсткости и т.п.).

Прочностной расчёт планетарных передач выполняют по формулам для цилиндрических передач. При определении расчётного момента, действующего в зубчатом зацеплении, учитывается число сателлитов, передающих рабочие нагрузки, и неравномерность нагружения их зубьев. Для жёсткой передачи без специальных мер выравнивания нагрузки в расчётные формулы вводят коэффициент неравномерности , а при использовании приёмов, выравнивающих нагрузку на зубьях сателлитов 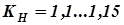. Далее расчёт ведут по наиболее нагруженному зацеплению.

КПД планетарной передачи можно подсчитать по формулам

для передачи с ведущим центральным колесом -	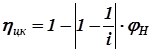;	(8.10)
для передачи с ведущим водилом -	;	(8.11)

где i – передаточное отношение планетарной передачи, j_Н – суммарный коэффициент потерь обращённой передачи (передачи, получающейся из рассчитываемой при дополнительном сообщении всем её звеньям угловой скорости равной скорости водила и навстречу ей направленной).

В свою очередь

; (8.12)

где j_п – потери в подшипниковых узлах передачи (для пары подшипников j_п=5×10^-3…1×10^-2); j_зп – коэффициент потерь в зубчатой паре; j_гп=6×10^-3…1×10^-2 – коэффициент, учитывающий затраты энергии на перемешивание смазки.

Потери энергии в зубчатом зацеплении

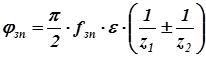; (8.13)

где f_зп – коэффициент трения в зубчатой паре (без смазки f_зп»0,2; со смазкой f_зп=0,08…0,15); e – коэффициент окружного перекрытия z₁ и z₂ – числа зубьев колёс, входящих в зубчатую пару. В формуле (8.13) знак «+» принимается для внешнего зацепления, «-» – для внутреннего.

Для изготовления элементов планетарных передач используют материалы, предназначенные для рядовых зубчатых передач, это, главным образом, углеродистые машиностроительные и углеродистые легированные стали, подвергаемые улучшающей термической обработке.

Как уже упоминалось выше, планетарные механизмы в исходном состоянии имеют две степени свободы, и это их свойство предопределило использование этих механизмов в качестве дифференцирующих (суммирующих). В режиме дифференциала работают планетарные суммирующие механизмы автомобильных дифференциалов с коническими колёсами, планетарные механизмы поворота гусеничных машин (БМП-2, БМП-3, танков, гусеничных тягачей и т.п.). Так, например, в многоцелевой гусеничной машине БМП-3 в качестве второго ведущего звена в механизме поворота используется эпицикл, что обеспечивает возможность изменения радиуса поворота машины в широких пределах без изменения её скорости движения.

Волновые передачи.

Волновыми называют механические передачи, включающие контактирующие между собой гибкое и жёсткое звенья и обеспечивающие передачу и преобразование движения при циклическом деформировании гибкого звена.

В технике применяется несколько видов волновых передач:

винтовые волновые передачи, предназначенные для преобразо­вания вращательного движения в поступательное и/или для передачи этого движения в загерметезированное пространство;

фрикционные волновые передачи, предназначенные для преобра­зования (чаще всего сильного редуцирования) вращательного движения и/или для передачи этого движения в загерметезированное пространство, и

зубчатые волновые передачи, имеющие аналогичное фрикционным предназначение, но способные передавать существенно большие мощности.

Рис. 8.3. Волновая зубчатая передача

Принцип использования волновой деформации для передачи и преобразования движения был предложен инженером А.И. Москвитиным в 1944 году для фрикционной передачи с электромагнитным генератором волн, а в 1959 году в США был выдан патент Уолтону Массеру (Walton Musser) на зубчатую передачу с механическим генератором волн. В дальнейшем для силовых передач нашли применение главным образом зубчатые волновые передачи, которые и будут рассмотрены в настоящей лекции.

Волновой механизм вращательного движения при соответствующем исполнении может использоваться в качестве редуцирующей передачи, мультипликатора или дифференциального механизма. Наиболее широкое распространение получили зубчатые волновые редукторы. Кинематически волновая передача может быть отнесена к группе планетарных передач, то есть волновую передачу следует рассматривать как планетарную, у которой одно из центральных колёс выполнено в форме гибкого зубчатого венца.

Гибкое колесо в волновой передаче в зависимости от конструкции генератора волн может нести одну, две, три и более волн деформации. Но, поскольку передаточное отношение волновой передачи не зависит от количества волн деформации на гибком колесе, а увеличение числа волн способствует росту изгибных напряжений в теле гибкого колеса, чаще всего используется симметричная двухволновая схема деформации гибкого колеса, позволяющая исключить возможность возникновения поперечных нагрузок на валах передачи.

В большинстве известных конструкций гибким является колесо с внешним зубчатым венцом, а жёсткое колесо снабжено внутренними зубьями (рис. 8.3). Такая волновая передача включает 3 основных звена: гибкое 1 и жёсткое 2 колёса и генератор волн H. Обычно бывает наиболее удобным конструктивно входной вал редуктора соединить с генератором волн, а выходной с гибким колесом, в этом варианте конструкция редуктора получается наиболее компактной и технологичной. Однако при передаче вращательного движения через герметичную стенку удобнее гибкое колесо сделать неподвижным, а выходной вал связать с жёстким колесом.

В недеформированном состоянии гибкое колесо волнового редуктора имеет диаметр и количество зубьев, меньшие по сравнению с жёстким колесом. При деформировании волновым генератором гибкое колесо удлиняется в направлении длинной оси кулачка генератора так, что его зубья входят в контакт с зубьями жёсткого колеса, вместе с тем вдоль короткой оси кулачка генератора гибкое колесо сжимается, и его зубья в этом направлении не могут взаимодействовать с зубьями жёсткого колеса. При вращении кулачка генератора волн последние пробегают по окружности зубчатого венца гибкого колеса, заставляя тем самым часть зубьев то входить в зацепление с зубьями жёсткого колеса, то выходить из него. За один оборот генератора волн в зацепление войдут все зубья жёсткого колеса, а так как число зубьев гибкого колеса z₁ несколько меньше числа зубьев жёсткого колеса z₂, гибкое колесо вынуждено будет сделать часть оборота равную разности чисел зубьев жёсткого и гибкого колёс z₂- z₁, но в противоположную вращению генератора волн сторону, следовательно, передаточное отношение составит

; (8.14)

а с учётом одинаковости модуля зацепляющихся колёс

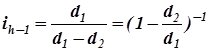. (8.14а)

Рассматривая аналогичным образом передачу движения в редукторе с неподвижным гибким колесом и подвижным, связанным с выходным валом, жёстким колесом не трудно установить, что передаточное отношение

. (8.15)

Разность в числах зубьев жесткого и гибкого колёс с целью исключения интерференции зубьев должна быть пропорциональна числу волн волнового генератора.

КПД волновых передач относительно высок и также как в планетарных передачах падает с увеличением передаточного числа, а с увеличением нагрузки вначале растёт до максимально возможной величины, а потом, при дальнейшем возрастании нагрузки, начинает резко снижаться. При оптимальной нагрузке в пределах передаточного числа 80£u£250 коэффициент полезного действия 0,9³h³0,8.

Достоинства волновых передач:

1. большое передаточное число (до 320, а в некоторых случаях и более);

2. большое число зубьев, одновременно находящихся в зацеплении (обычно от 40 до 80%) и, как следствие этого, большая нагрузочная способность – масса волнового редуктора меньше массы планетарного той же мощности, а объём может составлять около 30% от объёма последнего;

3. высокая кинематическая точность вследствие многозонности и многопарности зацепления, кинематическая погрешность передачи в некоторых случаях не превышает 0,5 мин;

4. высокий КПД, при больших передаточных числах превышающий КПД планетарных передач;

5. отсутствие поперечных нагрузок на валах вследствие симметричности конструкции;

6. возможность передачи движения в герметизированное пространство;

7. низкий уровень шума;

8. возможность использования в качестве дифференциального механизма;

9. малое число деталей и относительно низкая стоимость;

10. высокая технологичность изготовления.

Недостатки волновых передач:

1. невозможность получения низких значений передаточных чисел (для стальных гибких колёс u_min» 80, для пластмассовых - u_min» 20);

2. необходимость специального инструмента и оснастки для изгото­вления гибкого колеса, что затрудняет индивидуальное производство и ре­монт передач;

3. относительно низкий срок службы (срок службы стандартных волновых редукторов составляет около 10⁴ часов – чуть больше года непрерывной работы).

Гибкие колёса силовых редукторов изготавливают из легированных высокопрочных сталей 30ХГСА; 30ХГСН2А; 40ХНМА; 50С2 и некоторых других с термообработкой до 38…45 HRC и последующей шлифовкой диаметра, посадочного на подшипник генератора волн. Для изготовления остальных деталей применяются те же материалы, что и для рядовых зубчатых передач.

В военной технике волновые передачи нашли применение в приборах наведения и некоторых узлах боевых и вспомогательных машин.

Основной причиной выхода из строя волновых передач является поломка гибкого колеса и гибких колец подшипника генератора волн вследствие усталостного разрушения от действия знакопеременных изгибающих напряжений. Поэтому размеры передачи определяют исходя из предела выносливости на изгиб гибкого колеса и наружного кольца подшипника генератора волн.

Проектным расчётом определяется внутренний диаметр гибкого колеса по формуле

; (8.16)

где T₁ – вращающий момент на валу гибкого колеса, Н×м; [s] - допускаемые напряжения, МПа (для стали 30ХГСА [s]=150…170 МПа); E - модуль упругости материала колеса (для сталей можно принять E=2,1×10⁵ МПа) y_bd=b₁/d=0,15…0,20 – коэффициент ширины зубчатого венца; y_Sd=S₁/d=0,012…0,014 – коэффициент толщины зубчатого венца.

При использовании кулачкового генератора волн полученный расчётом диаметр округляется до ближайшего наружного диаметра гибкого подшипника. Далее определяются остальные параметры зубчатого зацепления по формулам, аналогичным с формулами цилиндрических передач.

Рассчитанное гибкое колесо: а) проверяется по напряжениям изгиба, изменяющимся по симметричному циклу в процессе деформирования колеса генератором волн; б) по напряжениям растяжения зубчатого венца, возникающим от действия на колесо тангенциальных сил и изменяющимся по отнулевому циклу, и по напряжениям кручения зубчатого венца, возникающим при передаче крутящего момента гибким колесом выходному валу и изменяющимся по отнулевому циклу.

Этой лекцией заканчивается рассмотрение механических передач. Представленные в настоящем цикле лекций передачи далеко не охватывают все возможные варианты строения и применения механических передач. Однако освоение заложенных в курсе основ подхода к их изучению позволит при необходимости самостоятельно разобраться с особенностями конструкции и работы вновь встреченных, ранее незнакомых механизмов.

Вопросы для самоконтроля:

1. Назовите главную особенность планетарной передачи.

2. Какие звенья составляют простой планетарный ряд?

3. В качестве каких механизмов может быть использован простой планетарный ряд?

4. Что называют кратностью простого планетарного ряда?

5. Какие основные свойства планетарного ряда позволяют использовать его в коробках передач?

6. Какие преимущества даёт использование планетарного ряда в коробке передач?

7. Назовите недостатки планетарной передачи.

8. Назовите главные условия, которые необходимо выполнить при создании планетарной передачи.

9. Какими свойствами передачи обусловлена возможная неравномерность загрузки сателлитов планетарного ряда?

10. Что необходимо предпринять для обеспечения равномерной загрузки сателлитов?

11. Какие особенности прочностного расчёта планетарного ряда?

12. Как установить КПД спроектированной планетарной передачи?

13. Используется ли планетарных механизм в качестве суммирующего, если да, то подтвердите примерами?

14. Назовите главную особенность волновой передачи.

15. Какие виды волновых передач Вы знаете?

16. Назовите основные элементы волновой передачи.

17. За счёт какого эффекта передаётся движение и нагрузка в волновой передаче?

18. Как подсчитать передаточное отношение в волновой передаче?

19. Назовите достоинства и недостатки волновой передачи.

20. Какой элемент волновой передачи наименее долговечен, какие материалы применяются для его изготовления?

21. Как выполняется проектный и проверочный расчёты волновой передачи?

é

Дата добавления: 2014-01-20