Интегрирование тригонометрических функций. I.Интеграл вида , где R(sin(x), cos(x)) – это рациональная функция относительно sin(x) и cos(x) подстановкой tg= t сводится к интегралу от рациональной

I. Интеграл вида , где R(sin(x), cos(x)) – это рациональная функция относительно sin(x) и cos(x) подстановкой tg= t сводится к интегралу от рациональной функции относительно t.

Действительно найдем.

= arctg(t);

x = 2 arctg(t); dx = ;

sin(x) = sin2= ;

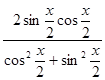разделим числитель и знаменатель на cos2; |tg= t|

sin(x) = ;

cos(x) = , делим на cos2;

cos(х) = ; тогда

= = ∫ r(t) dt, где r(t) – рациональная функция

относительно t.

r(t)

Пример: Вычислить.

= | tg= t | = = =

= 2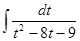 = -2= -2= ;

Такая подстановка называется универсальной, т.е. она пригодна для вычислений интеграла sin(x) и cos(x).

Замеяание1: часто применение универсальной подстановки приводит к громоздким вычислениям. Некоторые интегралы могут быть решены другим способом.

а) ∫ R(sin(x))cos(x) dx = | sin(x) =t; cos(x)dx = dt | = ∫ R(t) dt.

∫ R(t) dt – интеграл от рациональной функции относительно t.

б) ∫ R(cos(x))sin(x) dx = – ∫ R(t) dt;

в) ∫ R(tg(x)) dx = | tg(x)=t; x= arctg(t); dx = dt/(1+t2)| = = ∫r(t)dt,

r(t)

где r(t)- рациональная функция относительно t.

Пример: вычислить интеграл.

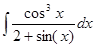= = |sin(x) = t; cos(x)dx=dt| = =

= _-t2 +1 |t+2 =∫(2 – t –3/(t+2))dt = 2t – t2/2 – 3 ln|t+2| = 2 sin(x)-1/2sin2x –3ln|sin(x)+2|+C

- t2-2t -t+2

_ 2t+1

2t+4

-3

Замечание2: если подынтегральная функция содержит sin(x) и cos(x) в четной степени и произведение sin(x)cos(x), то целесообразней применять подстановку tg(x) = t, тогда

x = arctg(t), dx = ;

;

;

sin(x)cos(x) = ;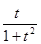

В результате получается рациональная функция относительно t.

Пример: = | tg(x) = t; dx = | =

= = = = =

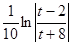== + C.

II. Интеграл вида

а)

I случай. m и n – положительные, одно из них нечетное.

Пусть m=2p+1, тогда ∫sin2p(x)cosn(x) sin(x)dx = – ∫(sin2x) p cosn(x) d(cos(x)) =

= – ∫(1 –cos2x) p cosn(x) d(cos(x)).

II.случай. m и n – целые, положительные, четные.

Пусть m=2p, n=2q, тогда

∫sinm(x)cosn(x)dx = ∫sin2p(x)cos2q(x)dx = ∫(sin2x) p(cos2x) qdx = ;

Возводя скобки в соответствующие степени и разбивая интеграл на сумму интегралов, в результате получаем интегралы либо типа а), либо типа б).

III.случай. m + n = –2k; tg(x)=t; ctg(x)=t;

Пример1:

I.случай. ∫sin5(x)cos2(x)dx = ∫sin4(x)cos2(x)sin(x)dx = –∫(sin2x) 2cos2(x)d(cos(x)) =

= –∫(1 – cos2x) 2cos2(x)d(cos(x)) = –∫(cos2x – 2 cos4x + cos6x)d(cos(x)) = –∫cos2(x)d(cos(x)) +

+ 2 ∫cos4(x)d(cos(x)) –∫cos6(x)d(cos(x)) = – cos3(x)/3 + 2 cos5(x)/5 – cos7(x)/7 +C.

Пример2:

∫sin4(x)cos2(x)dx = = 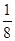∫(1 – cos2x)(1 – cos2(2x))dx =

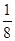= ∫(1 – cos2x)sin2(2x))dx = 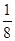∫sin2(2x))dx – 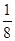∫cos2x∙sin2(2x))dx = –

– ∫sin2(2x))d(sin2x) = ∫dx – ∫cos(4x)dx – sin3(2x) = x – sin(4x) –

– sin3(2x) + C.

Пример3:

= ∫sin2(x)cos-6(x)dx = | m+n = 2-6 = 4| = =

= ∫ tg2(x)(1+tg2(x))d(tg(x)) = ∫ tg2(x)d(tg(x)) + ∫ tg4(x)d(tg(x)) = tg3(x)/3 + tg5(x)/5 + C.

Пример4:

= = = ∫ sin–6(x)cos–6(x) dx = | m=-6; n=-6; m+n=-12; | = = = == = |(1+x)n= 1 + nx +

+ | = = ∫ tg–6x d(tg(x)) +

+ ∫ tg–4x d(tg(x)) + ∫ tg–2x d(tg(x)) + ∫ d(tg(x)) + ∫ tg2x d(tg(x)) +

+ ∫ tg4x d(tg(x)) = (+ 5 tg2(x) + tg3(x)+ 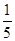tg5(x)) + C.

Дата добавления: 2014-01-20