Электрическое поле. Напряжённость поля. Вектор электрического смещения

Кулоновское взаимодействие между неподвижными электрически заряженными частицами или телами осуществляется посредством создаваемого ими электростатического поля. Оно представляет собой стационарное, т. е. не изменяющееся с течением времени, электрическое поле неподвижных электрических зарядов. Это поле является частным случаем электромагнитного поля, посредством которого осуществляется взаимодействие между электрически заряженными частицами, движущимися в общем случае произвольным образом относительно системы отсчета.

Характерное свойство электрического поля, отличающее его от других физических полей, состоит в том, что оно действует как на движущиеся, так и на неподвижные заряды (заряженные частицы и тела). Поэтому существование электрического поля можно обнаружить по его действию на неподвижные заряды.

Изучение электрического поля производится с помощью пробного заряда, т.е. положительного точечного заряда, при внесении которого исследуемое поле не искажается. Если в одну и ту же точку поля вносить различные пробные заряды, то на них будут действовать и различные силы. Однако отношение силы 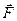, действующей на заряд, к величине 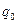этого заряда является постоянным для всех вносимых зарядов, независимо от их величины. Поэтому, это отношение принимают за силовую характеристику электрического поля в данной точке. Её называют напряжённостью и обозначают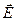

.(2.1)

Поскольку 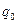заряд положительный, то из выражения (2.1) вытекает, что напряжённость поля равна силе, которая действует со стороны поля на положительный единичный заряд, и совпадает по направлению с направлением этой силы. В системе единиц СИ, как следует из (2.1), напряжённость измеряется в 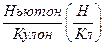или .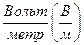

Найдем выражение для напряженности поля точечного электрического заряда 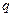, в точке, отстоящей от него, на расстоянии 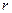. Поместим в эту точку пробный заряд 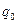. Проведем радиус-вектор 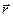из заряда 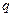к заряду 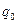. Тогда, подставляя значение силы по закону Кулона (1.3) в выражение для напряженности (2.1), получаем формулу для поля точечного заряда в векторной форме

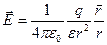.(2.2)

Из формулы (2.2) следует, что векторы напряженности электростатического поля точечного заряда 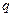во всех точках поля направлены радиально от заряда, если он положителен (q > 0),и к заряду, если он отрицателен (q < 0) (рис. 2.1).

Модуль напряженности поля точечного заряда может быть рассчитан с помощью выражения

. (2.3)

Таким образом, модуль напряжённости в любой точке электростатического поля, создаваемого точечным зарядом, пропорционален величине заряда и обратно пропорционален квадрату расстояния от заряда до точки, в которой определяется напряжённость.

Рис. 2.1

Для характеристики электрического поля наряду с напряженностью 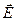вводят еще одну векторную величину 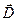, называемую электрическим смещением или электрической индукцией. Для поля в электрически изотропной среде связь 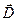и 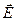в СИ имеет вид

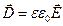. (2.4)

В СИ электрическое смещение выражается в кулонах на квадратный метр ().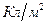

Дата добавления: 2014-01-20