Сегнетоэлектрики. 2 страница

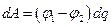. (19.1)

Полная работа, необходимая для сообщения конденсатору заряда 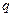находится по формуле

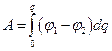. (19.2)

Учтем выражение (17.1) и запишем выражение (19.2) следующем виде

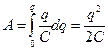. (19.3)

Очевидно, что электрическая энергия 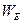заряженного конденсатора равна этой работе, т.е.

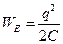. (19.4)

Учитывая, выражение (17.2), для емкости конденсатора, формулу (19.4) можно записать в ином виде

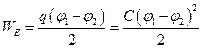. (19.5)

Энергия заряженного уединённого проводника равна работе, которую надо совершить против сил электростатического поля при переносе заряда из бесконечности, где потенциал условно принимается за нуль (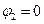), на проводник, потенциал которого 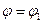. Поэтому электрическая энергия уединённого проводника, учитывая выражения (19.4) и (19.5), находится по формулам

. (19.6)

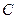где и 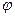— ёмкость и потенциал проводника.

Энергия заряженных проводников запасена в виде электрического поля. Поэтому целесообразно выразить её через напряжённость, 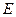характеризующую это поле. Это проще всего проделать для плоского конденсатора. В этом случае

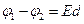и 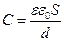, (19.7)

где 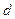— расстояние между обкладками, S — площадь каждой обкладки. Подставляя выражения (19.7) в (19.5), получаем

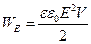. (19.5)

Здесь 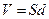— объём, занимаемый полем, равный объёму конденсатора.

Введём понятие объёмной плотности энергии. Являющейся абсолютной величиной, независящей от времени. Пусть энергия поля 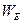равномерно распределена по объёму 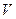. Тогда объёмная плотность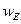

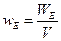, (19.6)

т.е. объёмная плотность энергии — это энергия поля в единице объёма. Измеряется данная величина в 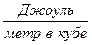(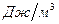). Если энергия поля распределена неравномерно, то надо выбрать элементарный объём 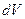, в пределах которого распределение энергии можно считать равномерным, и определить энергию 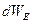поля в этом объёме. Тогда, согласно (19.6),

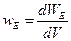, (19.7)

В случае конденсатора, заполненного однородным изотропным диэлектриком, объёмная плотность энергии, как следует из (19.5) и (19.6), находится по формуле

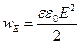. (19.7)

С учетом формулы (2.4) 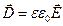, (19.7) примет вид

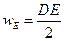. (19.8)

Эта формула справедлива не только для поля конденсатора, но и для других электрических полей, в том числе и переменных.

ГЛАВА 2. Электрический ток.

В разделе "Электростатика" (гл. 1) рассматривались свойства неподвижных зарядов и полей, создаваемых ими. Этот раздел представляет собой больше теоретический, чем практический интерес. В нём определяется ряд понятий, используемых в дальнейшем в науке об электричестве и магнетизме (электродинамике). В данной главе излагаются вопросы, связанные с электрическим током, значение которого в технике огромное.

§20. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА И ПЛОТНОСТЬ ТОКА.

Электрическим током называют любое упорядоченное движение электрических зарядов. Возможны различные виды тока. Наиболее важным является ток проводимости, который возникает внутри проводника, к которому приложено напряжение. Он представляет собой упорядоченное движение заряженных частиц (носителей тока) под действием электрического поля, созданного внутри проводника.

Для появления и существования тока проводимости необходимы два условия. Первое — наличие в данной среде носителей заряда, т.е. заряженных частиц, которые могли бы в ней перемещаться. Такими частицами в металлах являются электроны проводимости (свободные электроны); в жидких проводниках (электролитах) — положительные и отрицательные ионы; в газах — положительные и отрицательные ионы и электроны.

Второе — наличие в данной среде электрического поля, энергия которого затрачивалась бы на перемещение электрических зарядов. Для того чтобы ток был длительным, энергия поля должна все время пополняться, иными словами, нужен источник электрической энергии — устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.

В зависимости от свойств этих источников в электротехнике различают источники напряжения и источники тока. Поэтому во избежание недоразумений мы будем пользоваться в дальнейшем только термином «источник электрической энергии».

Упорядоченное движение зарядов можно осуществить и другим способом — перемещением в пространстве заряженного тела (проводника или диэлектрика). Такой электрический ток называется конвекционным. Например, движение по орбите Земли, обладающей избыточным отрицательным зарядом, можно рассматривать как конвекционный ток.

Исторически сложилось, что за направление электрического тока принимается направление движения положительно заряженных частиц (положительных зарядов). Поэтому, если ток обусловлен упорядоченным движением отрицательно заряженных частиц, то направление тока считается противоположно направленным движению этих частиц.

Для характеристики электрического тока через какую-либо поверхность (например, в случае тока проводимости — через поперечное сечение проводника) вводится понятие силы тока. Силой тока называется физическая величина , равная отношению заряда , переносимого через рассматриваемую поверхность 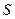за малый промежуток времени 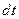, к величине этого промежутка:

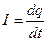. (20.1)

Если сила тока и его направление не изменяются с течением времени, то ток называется постоянным. Сила постоянного тока

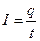. (20.2)

где 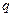— заряд, переносимый через поверхность 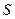за конечный промежуток времени .

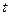Для того чтобы ток проводимости был постоянным, заряды не должны накапливаться или убывать ни в одной части проводника. Поэтому цепь постоянного тока должна быть замкнутой, а суммарный электрический заряд, который поступает за одну секунду сквозь поверхность 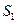в объем проводника, заключенный между двумя произвольно выбранными поперечными сечениям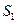и и (рис. 20.1), должен быть равным суммарному заряду, выходящему из этого объема за то же время сквозь поверхность . Таким образом, сила постоянного тока во всех сечениях проводника одинакова.

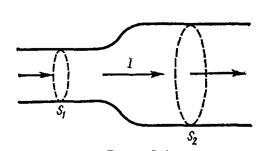рис. 20.1

Единица силы тока в СИ — ампер (А) — определяется на oсновании электромагнитного взаимодействия двух параллельных прямолинейных постоянных токов. Из формулы (20.2) следует, что один ампер равен силе постоянного электрического тока, при котором через любое поперечное сечение проводника переносится заряд, равный ().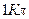

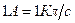Для характеристики направления электрического тока в различных точках рассматриваемой поверхности и распределения силы тока по этой поверхности вводится вектор плотности тока. Вектор плотности электрического тока 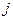совпадает по направлению с движением положительно заряженных частиц — носителей заряда и численно равен отношению силы тока 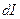сквозь малый элемент поверхности, нормальный к направлению движения заряженных частиц, к площади 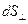этого элемента:

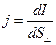. (20.3)

В СИ плотность тока измеряется в амперах на квадратный метр ().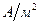

Выразим силу и плотность тока через скорость 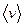упорядоченного движения зарядов в проводнике. Если концентрация носителей тока равна 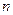каждый носитель имеет элементарный заряд 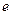, то за время 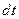через поперечное сечение 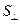проводника переносится заряд

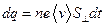. (20.4)

Сила тока

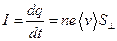, (20.5)

а плотность тока

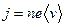. (20.6)

Найдем связь между плотностью тока 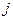и силой тока 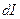через малый элемент 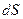поверхности, нормаль к которому составляет с 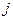угол 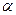. Площадь 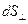проекции площадки 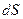на плоскость, нормальную к 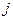, равна 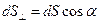. Поэтому в соответствии с (20.3)

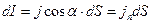или 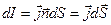, (20.7)

где 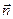— единичный вектор, перпендикулярный площадке 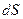, 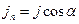— проекция вектора 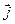на направление нормали 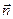, 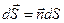— вектор элементарной площадки.

Из формул (20.7) следует, что сила тока через произвольную поверхность 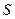равна

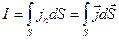, (20.8)

где интегрирование проводится по всей площади этой поверхности. В дальнейшем при нахождении силы тока проводимости мы будем рассматривать поперечные сечения проводника, для которых 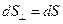и 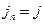, так что

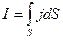, (20.9)

Опыты показали, что плотность постоянного тока одинакова по всему поперечному сечению 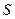однородного проводника. Поэтому для постоянного тока формулу (20.9) можно записать в виде

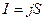. (20.10)

§21. Сторонние силы. ЭДС и напряжение.

Возьмём два проводника, заряженные разноимёнными зарядами, и соединим их другим проводником. Тогда в этом проводнике за счёт разности потенциалов на его концах возникает электрическое поле (поле кулоновских сил), под действием которого свободные заряды (носители тока) приходят в упорядоченное движение от положительного потенциала к отрицательному (имеется в виду движение положительных зарядов, поскольку за направление тока принимается движение именно этих зарядов), т.е. возникает электрический ток. Однако этот ток очень быстро прекращается в силу того, что протекание тока приводит к выравниванию потенциалов на концах проводника и к исчезновению внутри него электрического поля. Т.о. если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение носителей от точек с большим потенциалом к точкам с меньшим потенциалом. Это приводит к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками тока.

Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними. Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и т. п.

Роль источника тока в электрической цепи, образно говоря, такая же, как роль насоса, который необходим для перекачивания жидкости в гидравлической системе. Под действием создаваемого поля сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддерживается разность потенциалов и в цепи течет постоянный электрический ток.

Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой 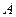, совершаемой сторонними силами при перемещении единичного положительного заряда 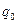, называется электродвижущей силой (ЭДС), действующей в цепи:

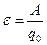(21.1)

Единица измерения ЭДС в системе СИ является Вольт ()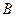

Сторонняя сила 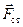, действующая на заряд 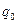, может быть выражена как

, (21.2)

где 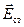— напряженность поля сторонних сил.

Работа сторонних сил по перемещению заряда 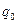на замкнутом участке цепи

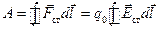, (21.3)

Разделив (21.3) на 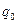, получим выражение для ЭДС, действующей в цепи:

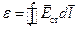, (21.4)

т.е. ЭДС, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил. ЭДС, действующая на участке 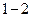, равна

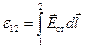. (21.5)

На заряд 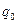помимо сторонних сил действуют также силы электростатического поля 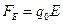. Таким образом, результирующая сила, действующая в цепи на заряд 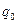, равна

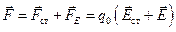. (21.6)

Работа, совершаемая результирующей силой над зарядом 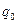на участке 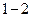, равна

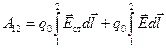. (21.7)

Выражение (21.7) можно представить в следующем виде

. (21.8)

Для замкнутой цепи работа электростатических сил равна нулю, поэтому в данном случае

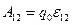. (21.9)

Напряжением 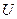на участке 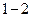называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи. Т.о., согласно (21.8),

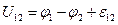. (21.8)

В СИ напряжение выражается в вольтах. Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует ЭДС, т. е. сторонние силы отсутствуют.

§22. Сопротивление проводников. Закон Ома для однородного участка цепи и для полной цепи.

Немецкий физик Г. Ом (1787 —1854) экспериментально установил, что сила тока , текущего по однородному металлическому проводнику (т.е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению 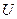на концах проводника

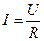, (22.1)

где 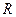— электрическое сопротивление проводника.

Уравнение (22.1) выражает закон Ома для участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. В данном законе сопротивление является коэффициентом пропорциональности между силой тока и напряжением, и не зависит от них.

Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Как было указано выше сопротивление обозначается 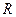. Сопротивление скалярная величина. Формула (22.1) позволяет установить единицу сопротивления Ом: 1Ом — сопротивление такого проводника, в котором при напряжении 1В течет постоянный ток 1А.

Для однородного линейного проводника сопротивление 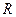прямо пропорционально его длине 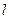и обратно пропорционально площади его поперечного сечения :

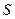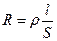, (22.2)

где 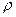— коэффициент пропорциональности, характеризующий материал проводника и называемый удельным электрическим сопротивлением. Единица удельного электрического сопротивления — 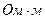. Наименьшим удельным сопротивлением обладают серебро () и медь (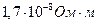). На практике наряду с медными применяются алюминиевые провода. Хотя алюминий и имеет большее, чем медь, удельное сопротивление (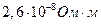), но зато обладает меньшей плотностью по сравнению с медью.

В физике применяются величины обратные сопротивлению и удельному сопротивлению - это проводимость (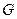) и удельная проводимость (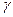), соответственно.

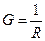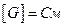, (сименс) (22.3)

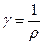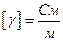. (22.4)

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (22.2) в закон Ома (22.1), получим

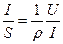. (22.5)

Учитывая, что напряженность электрического поля в проводнике равна

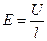, (22.6)

а плотность тока,

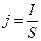, (22.7)

формулу (22.5) можно записать в виде

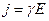. (22.8)

Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора 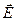, то направления 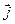и 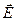совпадают. Поэтому формулу (22.8) можно записать в виде

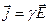. (22.9)

Выражение (22.9) — закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Рассмотрим замкнутую электрическую цепь, состоящую из сопротивления 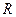и источника тока 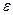(рис.22.1). Найдем зависимость между электродвижущей силой источника тока 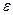и силой тока . Сопротивление 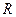проводника, соединяющего полюсы источника тока, принято называть внешним, а сопротивление 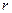самого источника тока — внутренним сопротивлением. Из формулы (21.8) 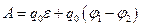выразим :

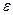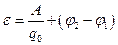, (22.10)

или, учитывая что 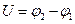, (22.10) запишется в следующей форме

, (22.10)

где 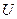— напряжение на внешнем сопротивлении, 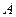— работа перемещения заряда 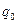внутри источника тока, т. е. работа тока на внутреннем сопротивлении 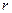. Тогда, с учетом выражений 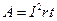(будет получена в §25), где 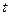- время, 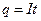и 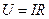, формулу (22.10) можно записать в виде

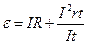, (22.11)

откуда

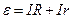. (22.12)

Рисунок с ЭДС и резистором рис.22.1

Так как, согласно закону Ома (22.1), произведения 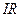и 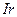представляют собой падения напряжения на внешнем и на внутреннем участке цепи, то соотношению (22.12) можно дать следующее толкование: в замкнутой электрической цепи электродвижущая сила источника тока равна сумме падений напряжения на всех участках цепи.

Приведя соотношение (22.12) к виду

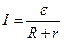. (22.13)

получим выражение закона Ома для замкнутой электрической цепи: сила тока пропорциональна электродвижущей силе и обратно пропорциональна полному сопротивлению цепи .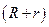

§23. Параллельное и последовательное соединение проводников.

Возможны два варианта простейших соединений проводников – это параллельное и последовательное. При расчете сопротивлений более сложных соединений проводников их сводят к комбинации двух вышеуказанных.

Рис. 23.1(добавить напряжение)

Рассмотрим сначала последовательное соединение (рис. 23.1). При последовательном соединении заряд не теряется и не накапливается ни на одном из участков цепи, следовательно, сила тока во всех проводниках одинакова,

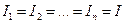. (23.1)

Общее напряжение складывается из напряжений каждого участка

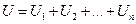. (23.2)

Воспользуемся законом Ома для участка цепи (22.1) 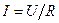и выразим напряжение на каждом участке и для всей цепи:

Дата добавления: 2014-01-20