Кинематическое исследование механизмов

Кинематическое исследование – исследование трёх величин – перемещения, скорости и ускорения какой-либо точки интересующего нас звена.

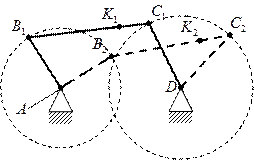Цикл – время движения ведущего звена в машине, после которого положение звеньев повторяется.

Определение скоростей. Понятие о теореме подобия для определения скоростей отдельных точек звеньев.

Представим себе плоское движение.

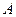Модуль скорости точки можно определить по формуле: 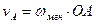, а линия действия этого вектора будет перпендикулярная отрезку .

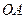Модуль скорости точки можно определить по формуле: 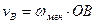, а линия действия этого вектора будет перпендикулярная отрезку .

Модуль скорости точки 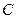можно определить по формуле: 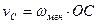, а линия действия этого вектора будет перпендикулярная отрезку .

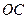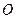- мгновенный центр вращения.

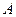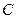Видно, что модули скоростей точек , и пропорциональны длинам отрезков 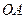, и 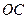, то есть: .

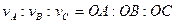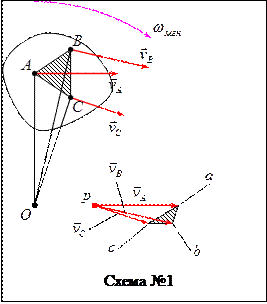
Многоугольник 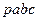подобен многоугольнику 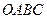, так как он образован взаимно перпендикулярными и пропорциональными прямыми. Поэтому Схема №1 представляет собой план скоростей треугольника 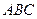, то есть треугольник 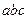является планом скоростей треугольника .

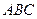План скоростей жёсткого звена – геометрическое место точек концов векторов абсолютных скоростей любых точек звена, если они построены из одной общей точки 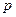, называемой полюсом плана скоростей.

План скоростей всегда строится в масштабе. В дисциплине «Теория машин и механизмов» масштаб имеет размерность, поэтому его принято называть масштабным коэффициентом: , .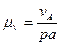

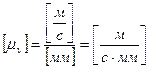План скоростей подобен самому звену, и повёрнут на девяносто градусов в сторону мгновенного вращения.

Если план скоростей жёсткого звена подобен своему звену, то план скоростей механизма не подобен самому механизму, так как в отличие от жёсткого звена механизм есть изменяемая подвижная система.

План скоростей механизма – совокупность планов скоростей отдельных звеньев, построенных из одной общей точки 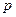, называемой полюсом плана скоростей.

Дано: , 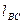и .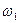

Требуется определить: .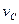

Зададимся неким масштабным коэффициентом .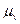

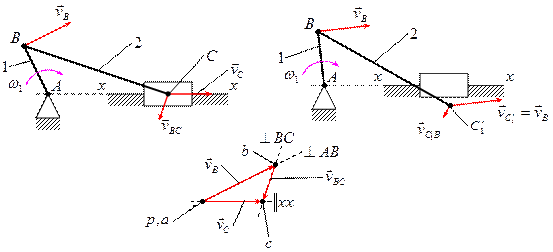
Для построения плана скоростей механизма существуют различные методы, наиболее распространённым из которых является метод векторных уравнений, разработанный советскими учёными.

Модуль скорости точки можно определить по следующей формуле: 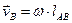. Линия действия вектора скорости точки перпендикулярна звену 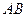, а сам вектор направлен в сторону вращения звена .

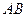Допустим, что точка 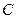не закреплена, и представим себе, что все точки звена 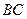совершают переносное движение со скоростью 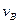, то есть 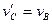. С одной стороны 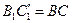, с другой стороны .

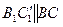Вернём точку 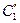на действительную траекторию 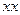, для чего придадим точке 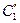скорость относительного вращательного движения около точки 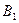со скоростью относительного движения .

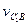На плане скоростей векторы, исходящие из полюса скоростей 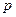являются векторами абсолютных скоростей соответствующих точек, а векторы, которые не проходят через полюс плана ускорений, являются относительных скоростей соответствующих точек. Отрезок 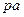является планом скоростей звена 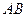, а отрезок 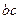является планом скоростей звена .

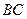Дата добавления: 2014-01-20