
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
КПД червячных передач
|
|
|
|
Его различают в зависимости от того, какое звено является ведущим – червяк или червячное колесо. Если ведущим является червяк, то: 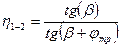 . Эта формула используется только в случае, когда
. Эта формула используется только в случае, когда 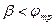 . Если ведущим является червячное колесо, то:
. Если ведущим является червячное колесо, то: 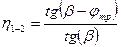 . Эта формула действует только тогда, когда
. Эта формула действует только тогда, когда 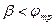 .
.
Синтез схем четырёхшарнирных рычажных механизмов.
 Прототипами таких механизмов могут служить схемы станков-качалок.
Прототипами таких механизмов могут служить схемы станков-качалок.
Существуют различные потребности к созданию схем таких механизмов. Наиболее распространённой является проектирование четырёхшарнирного рычажного механизма по заданному коэффициенту изменения средней скорости выходного звена (рабочего звена). В данном случае таковым является коромысло 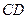 . Ведущим в данном механизме считаем кривошип
. Ведущим в данном механизме считаем кривошип 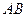 .
. 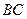 - шатун. Длина коромысла и максимальный угол качания заданы. Требуется определить размеры кривошипа и найти расстояние
- шатун. Длина коромысла и максимальный угол качания заданы. Требуется определить размеры кривошипа и найти расстояние  .
.
При переходе коромысла из крайнего правого положения в крайнее левое положение, кривошип из точки 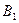 перейдёт в положение
перейдёт в положение 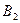 и пройдёт угол
и пройдёт угол 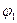 . При переходе из крайнего левого положения в крайнее правое положение, кривошип перейдёт из точки
. При переходе из крайнего левого положения в крайнее правое положение, кривошип перейдёт из точки 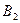 в точку
в точку 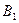 и пройдёт угол
и пройдёт угол 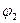 . Кривошип обладает постоянной угловой скоростью
. Кривошип обладает постоянной угловой скоростью 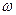 . Так как скорость постоянна, то очевидно, что
. Так как скорость постоянна, то очевидно, что 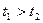 .
.
 Средние скорости кривошипа можно определить по формулам:
Средние скорости кривошипа можно определить по формулам: 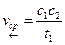 ;
; 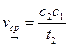 . Так как
. Так как 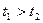 , то
, то 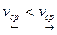 . Тогда отношение скоростей:
. Тогда отношение скоростей:  - коэффициент неравномерности или коэффициент изменения средней скорости.
- коэффициент неравномерности или коэффициент изменения средней скорости.
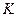 - коэффициент изменения скорости при движении ведомого звена влево и вправо, этот коэффициент можно определить по следующей формуле:
- коэффициент изменения скорости при движении ведомого звена влево и вправо, этот коэффициент можно определить по следующей формуле: 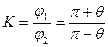 , откуда угол
, откуда угол 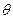 можно определить по формуле:
можно определить по формуле: 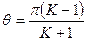
Часто необходимо иметь такую неравномерность движения, которая диктуется технологическими требованиями рабочего процесса, когда время на холостой ход можно сократить кинематическим способом. Рабочий ход происходит с необходимой для процесса скоростью и в заданное время. Такой механизм позволяет сохранить холостой ход. При проектировании нового механизма движение ведомого звена (чаще всего оно является рабочим) задаётся с различными скоростями, то есть задаётся коэффициент 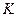 , при этом задаются длиной коромысла и максимальным углом качания. Требуется определить положение центра вращения кривошипа и длины кривошипа и шатуна, чтобы соблюдался заданный коэффициент
, при этом задаются длиной коромысла и максимальным углом качания. Требуется определить положение центра вращения кривошипа и длины кривошипа и шатуна, чтобы соблюдался заданный коэффициент 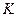 .
.
Имея заданный размер коромысла и угол его качания строим крайние положения. Определяем угол 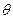 по заданному коэффициенту
по заданному коэффициенту 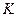 , с помощью формулы
, с помощью формулы 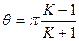 . Соединим
. Соединим 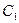 с
с 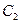 соответствующей хордой. Из точки
соответствующей хордой. Из точки 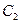 опустим перпендикуляр
опустим перпендикуляр 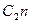 к хорде и построим угол
к хорде и построим угол  , который равен
, который равен 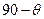 . Через точки
. Через точки 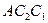 проведём окружность
проведём окружность 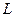 . Лучи проведённые из любой точки этой окружности будут образовывать один и тот же угол
. Лучи проведённые из любой точки этой окружности будут образовывать один и тот же угол 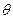 .
.
 , где
, где  ;
; 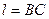 .
.
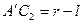 , где
, где  ;
; 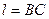 .
.
Длину кривошипа можно определить следующим способом: 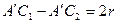 . Раствором циркуля равным
. Раствором циркуля равным 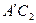 проведём дугу до пересечения с прямой
проведём дугу до пересечения с прямой  и получим точку
и получим точку 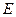 . Тогда
. Тогда 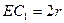 , откуда
, откуда  .
.
Построения, произведённые в масштабе, дадут нам реальную длину кривошипа, которую можно определить следующим образом: 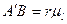 . Углы
. Углы 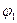 и
и 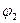 определяются из формул:
определяются из формул:  и
и  . Длины звеньев
. Длины звеньев 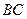 и
и  можно определить по следующим формулам:
можно определить по следующим формулам: 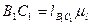 и
и 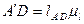 соответственно.
соответственно.
Таким образом все геометрические параметры механизма определены.
Чтобы определить оптимальное положение центра вращения кривошипа 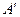 следует учитывать дополнительное требование. Таковым является угол давления
следует учитывать дополнительное требование. Таковым является угол давления 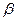 . Этот угол должен лежать в пределах от
. Этот угол должен лежать в пределах от 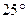 до
до 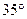 . Точка
. Точка 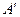 для центра вращения кривошипа должна лежать всегда левее (в случае нашего механизма) угла
для центра вращения кривошипа должна лежать всегда левее (в случае нашего механизма) угла 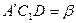 .
.
Построим планы скоростей для определения максимальных скоростей точки 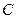 коромысла при движении влево и вправо.
коромысла при движении влево и вправо.
Максимальная скорость будет в тех положениях, когда расположение кривошипа и шатуна будет взаимно перпендикулярным, то есть звено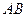 будет перпендикулярно звену
будет перпендикулярно звену 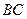 , как показано на рисунке.
, как показано на рисунке.

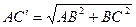 ;
;
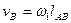 ;
; 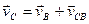 .
.
Имея планы скоростей можно проверить правильность выдерживания коэффициента изменения скорости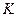 .
.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 302; Нарушение авторских прав?; Мы поможем в написании вашей работы!