Общий прием вычисления динамического коэффициента при ударе

Предположим, что очень жесткое тело А весом Q, деформацией которого можно пренебречь, падая с некоторой высоты H, ударяет по другому телу B, опирающемуся на упругую систему С (рис.2). В частном случае это может быть падение груза на конец призматического стержня, другой конец которого закреплен (продольный удар), падение груза на балку, лежащую на опорах (изгибающий удар), и т. п.

Рис.2. Динамическая модель ударного нагружения.

В течение очень короткого промежутка времени упругая система С испытает некоторую деформацию. Обозначим через перемещение тела В (местной деформацией которого пренебрежем) в направлении удара. В упомянутых частных случаях при продольном ударе за перемещение соответственно нужно считать продольную деформацию стержня 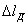, при изгибающем ударе — прогиб балки в ударяемом сечении и т. п. В результате удара в системе С возникнут напряжения 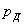( или — в зависимости от вида деформации).

Полагая, что кинетическая энергия Т ударяющего тела полностью переходит в потенциальную энергию деформации упругой системы, можем написать:

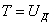
(1)

Так как к моменту окончания деформации ударяющее тело пройдет путь , то его запас энергии будет измеряться произведенной им работой и будет равен:

(2)

Вычислим теперь . При статической деформации потенциальная энергия 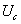численно равна половине произведения действующей силы на соответствующую деформацию:

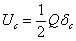
(3)

Статическая деформация 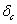в ударяемом сечении может быть вычислена по закону Гука, который в общем виде можно записать так:

или

Здесь с — некоторый коэффициент пропорциональности (называемый иногда жесткостью системы); он зависит от свойств материала, формы и размеров тела, вида деформации и положения ударяемого сечения. Так, при простом растяжении или сжати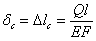и , и 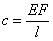; при изгибе балки, шарнирно закрепленной по концам, сосредоточенной силой Q посредине пролета и ; и т.д.

Таким образом, выражение для энергии может быть переписано так:

В основу этой формулы положены две предпосылки: а) справедливость закона Гука и б) постепенный — от нуля до окончательного значения — рост силы Q, напряжений 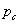и пропорциональных им деформаций .

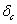Опыты с определением модуля упругости по наблюдениям над упругими колебаниями стержней показывают, что и при динамическом действии нагрузок закон Гука остается в силе, и модуль упругости сохраняет свою величину. Что касается характера нарастания напряжений и деформаций, то и при ударе деформация происходит, хотя и быстро, но не мгновенно; постепенно растет в течение очень короткого промежутка времени от нуля до окончательного значения; параллельно росту деформаций возрастают и напряжения .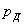

Реакция системы С на действие упавшего груза Q (назовем ее ) является следствием развития деформации ; она растет параллельно от нуля до окончательной, максимальной величины и, если напряжения 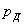не превосходят предела пропорциональности материала, связана с ней законом Гука:

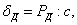
где с — упомянутый выше коэффициент пропорциональности, сохраняющий свое значение и при ударе.

Таким образом, обе предпосылки для правильности формулы (3) принимаются и при ударе. Поэтому можно считать, что вид формулы для при ударе будет тот же, что и при статическом нагружении системы С силой инерции , т. е.

(Здесь учтено, что по предыдущему .) Подставляя значения Т и в уравнение (1), получаем:

или

Отсюда

или, удерживая перед радикалом для определения наибольшей величины деформации системы в направлении удара знак плюс, получаем:

(4)

Так как напряжения и усилия по закону Гука пропорциональны деформации, то

	(5)
	(6)

Из этих формул видно, что величина динамических деформаций, напряжений и усилий зависит от величины статической деформации, т. е. от жесткости и продольных размеров ударяемого тела; ниже это дополнительно будет показано на отдельных примерах. Величина

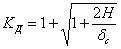
(7)

в данном случае представляет собой динамический коэффициент.

Заменяя в этой формуле Н на 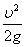, где — скорость ударяющего тела в начальный момент удара, получаем:

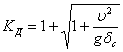
(8)

Кроме того, так как

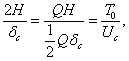
где —энергия ударяющего тела к моменту начала удара, то выражение для динамического коэффициента может быть представлено еще и в таком виде:

(9)

Если мы в формулах (4) и (5) положим , т. е. просто сразу приложим груз Q, то и ; при внезапном приложении силы Q деформации и напряжения вдвое больше, чем при статическом действии той же силы.

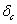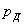Наоборот, если высота падения груза Н (или скорость ) велика по сравнению с деформацией , то в подкоренном выражении формул (4) — (8) можно пренебречь единицей по сравнению с величиной отношения . Тогда для и получаются следующие выражения:

и

(10)

При очень большой величине отношения можно пренебречь и единицей, стоящей перед корнем, т. е. написать:

и

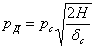
(11)

Динамический коэффициент в этом случае определяется по формуле

(12)

Необходимо отметить, что в то время как пренебрежение единицей 2Н в подкоренном выражении допустимо уже при (неточность приближенных формул будет не больше 5%). пренебрежение единицей, стоящей перед корнем, допустимо лишь при очень большой величине отношения .

Так, например, для того чтобы приближенные формулы (11) и (12) давали погрешность не более 10%, отношение должно быть больше 110.

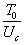Формулы и , в которых выражается через , могут быть использованы также для решения задачи о встречном ударе тел, двигающихся с некоторой скоростью, при определении напряжений в цилиндре двигателя внутреннего сгорания, вызванных резким повышением давления газа при вспышке горючей смеси и др. На этом основании их можно считать общими формулами для расчета на удар.

Обобщая сказанное выше, можем наметить следующий общий прием решения задач на определение напряжений при ударе. Применяя закон сохранения энергии, надо:

1) вычислить кинетическую энергию ударяющего тела Т;

2) вычислить потенциальную энергию тел, воспринимающих удар, под нагрузкой их силами инерции при ударе; потенциальная энергия должна быть выражена через напряжение (,) в каком-либо сечении, через деформацию (удлинение, прогиб) или через силу инерции ударяющего тела;

3) приравнять величины и Т и из полученного уравнения найти или непосредственно динамическое напряжение, или деформацию, а по ней, пользуясь законом Гука, напряжение или силу и соответствующие ей динамические напряжения и деформации.

Описанный общий прием расчета на удар предполагает, что вся кинетическая энергия ударяющего тела целиком переходит в потенциальную энергию деформации упругой системы. Это предположение не точно. Кинетическая энергия падающего груза частично превращается в тепловую энергию и энергию неупругой деформации основания, на которое опирается система.

Вместе с тем при высоких скоростях удара деформация за время удара не успевает распространиться на весь объем ударяемого тела и в месте удара возникают значительные местные напряжения, иногда превосходящие предел текучести материала. Так, например, при ударе свинцовым молотком по стальной балке большая часть кинетической энергии превращается в энергию местных деформаций. Подобное же явление может иметь место даже и в том случае, когда скорость удара мала, но жесткость или масса ударяемой конструкции велика.

Указанные случай соответствуют большим величинам дроби . Поэтому можно сказать, что описанный выше метод расчета применим, пока дробь не превышает определенной величины. Более точные исследования показывают, что ошибка не превышает 10% если 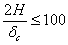. Так как эта дробь может быть представлена в виде отношения 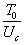, то можно сказать, что изложенный метод применим, пока энергия удара превышает не более чем в 100 раз потенциальную энергию деформации, соответствующую статической нагрузке конструкции весом ударяющего груза. Учет массы ударяемого тела при ударе позволяет несколько расширить пределы применимости этого метода в тех случаях, когда масса ударяемого тела велика.

Более точная теория удара излагается в курсах теории упругости.

Лекция № 50. Оценка прочности при ударной нагрузке.

Вид формул, полученных для динамического коэффициента, показывает, какие большие качественные различия ведет за собой количественное изменение периода действия силы на тело.

Рассмотрим некоторые случаи удара при простейших деформациях. При этом для нахождения коэффициента динамичности применим основные полученные формулы для динамического коэффициента.

Для определения , 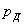и используем зависимости:

и

В случае продольного растягивающего или сжимающего удара (Рис 1)

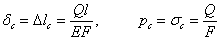
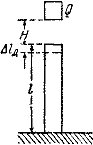
Рис.1. Модель продольного удара.

Для вычисления динамического коэффициента может быть выбрано одно из следующих выражений:

После этого без затруднений вычисляются 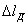, и .

Приближенная формула для вычисления напряжений в данном частном случае получает такой вид:

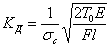и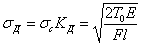

Замечаем, что как при статической, так и при динамической нагрузке напряжение в сжатом стержне зависит от величины сжимающей силы и от площади поперечного сечения стержня.

Но при статическом действии груза Q передающаяся на стержень сила равна Q и не зависит от размеров и материала стержня, при ударе же величина силы , вызывающей напряжения в стержне, зависит от ускорения, передающегося от ударяемого тела на ударяющее, т. е. от величины промежутка времени, в течение которого изменяется скорость ударяющего тела. В свою очередь этот промежуток времени зависит от величины динамической продольной деформации 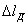, от податливости стержня. Чем эта величина больше, т. е. чем меньше модуль Е и чем больше длина стержня l, тем больше продолжительность удара, меньше ускорение и меньше давление .

Таким образом, при равномерном распределении напряжений, одинаковом во всех сечениях стержня, динамическое напряжение будет уменьшаться с увеличением площади поперечного сечения стержня и с увеличением его податливости (т. е. с увеличением длины и уменьшением модуля упругости Е); именно поэтому смягчают удар всякие рессоры и пружины, расположенные между ударяющимися деталями. Все это и отражают приведенные выше формулы. В частности, с известным приближением можно считать, что при продольном ударе величина напряжений зависит уже не от площади, а от объема стержня.

Вычислив величину динамического напряжения, мы можем теперь написать условие прочности в виде

где []—допускаемая величина нормальных напряжений при ударе, равная для пластичного материала . Величину коэффициента запаса можно было бы выбрать равной величине основного коэффициента запаса при статическом действии нагрузок, так как динамичность нагрузки уже отражена. Однако, ввиду некоторой упрощенности изложенного метода расчета, этот коэффициент принимают несколько повышенным — до 2. Кроме того, обычно в этих случаях применяют материал более высокого качества (в отношении однородности и пластических свойств).

При изгибе величина статической деформации 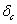, представляющей собой статический прогиб балки 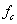с в месте удара, зависит от схемы нагружения и условий опирания балки.

Так например, для балки пролетом l, шарнирно закрепленной по концам и испытывающей посредине пролета удар от падающего с высоты Н груза Q (Рис.2, а),

а) двухопорная балка, б) консольная
Рис.2. Модели удара:

получаем:

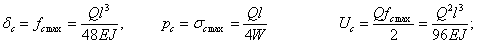
для консоли, испытывающей удар от груза Q, падающего на свободный конец консоли (Рис 2, б):

Подставляя в формулу для коэффициента динамичности значения или 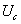, находим , а затем и величину динамических напряжений и деформаций. Так например, в случае балки на двух опорах при вычислении динамического напряжения имеем такую формулу:

Условие прочности в этом случае напишется:

Приближенные формулы для вычисления 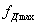и в случае удара по балке на двух опорах получают такой вид:

Аналогичные выражения для 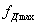и получаются и в случае удара по консоли. Имея в виду, что

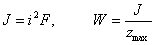
и

можем представить выражение для еще и в таком виде:

Из последней приближенной формулы видно, что динамические напряжения при изгибе балки зависят от модуля упругости материала, объема балки, формы ее поперечного сечения (отношение ), а также от схемы нагружения и условий опирания балки (в данном случае в подкоренном выражении стоит ; для балок, иначе загруженных и закрепленных, числовой коэффициент у будет другим). Таким образом, в балке прямоугольного сечения высотой h и шириной b, поставленной на ребро или положенной плашмя, наибольшие напряжения при ударе будут одинаковы и равны (по приближенной формуле):

так как в обоих случаях

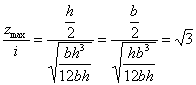
Как известно, при одинаковой статической нагрузке наибольшие напряжения в балке, положенной плашмя, будут в отношении больше, чем напряжения в балке, поставленной на ребро. Сказанное выше, разумеется, справедливо лишь до тех пор, пока явление удара происходит в пределах упругости.

Сопротивление балок ударным нагрузкам зависит и от момента сопротивления и от жесткости балки. Чем больше податливость, деформируемость балки, тем большую живую силу удара она может принять при одних и тех же допускаемых напряжениях. Наибольший прогиб балка дает в том случае, когда во всех ее сечениях наибольшие напряжения будут одинаковыми, т. е. если это будет балка разного сопротивления; такие балки при одном и том же допускаемом напряжении дают большие прогибы, чем балки постоянного сечения, и значит, могут поглощать большую энергию удара. Поэтому рессоры обычно и делают в форме балок равного сопротивления.

Рассмотрим теперь задачу определения напряжений при скручивающем ударе.

Если вращающийся вал внезапно останавливается торможением одного из его концов, а на другом его конце на него передается живая сила маховика , скручивающая вал, то напряжения также могут быть определены указанным выше методом. Вал будет скручиваться двумя парами сил (силы инерции маховика и силы торможения) с моментом М.

В данном случае

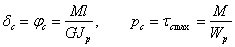
и

Следовательно,

и

так как

и

И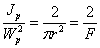мея в виду, что живая сила маховика T₀ равна

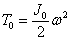
где 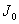— момент инерции массы маховика, а — угловая скорость, можем написать:

Замечаем, что и при скручивающем ударе наибольшие напряжения зависят от модуля упругости и от объема вала.

Дата добавления: 2014-01-20