Передаточное отношение цилиндрических редукторов

Как указывалось в п. 4.2.1., передаточным отношением называется отношение угловых скоростей зубчатых колес:

U₁₂ = ω₁/ω₂. (4.17)

Зубчатые колеса в передаче могут соединяться по-разному. В случае одноступенчатой передачи для внешнего зацепления передаточное отношение имеет отрицательный знак, т.к. колеса вращаются в разные стороны

U₁₂= - ω₁/ω₂.

Для внутреннего зацепления передаточное отношение имеет положительный знак, т.к. угловые скорости колес направлены в одну сторону

U₁₂= + ω₁/ω₂.

Передаточное отношение можно определять также через отношение чисел зубьев колес, которыми обычно и задаются:

U₁₂ = ± z₂/z₁. (4.18)

Передаточное отношение многоступенчатого зубчатого механизма есть произведение взятых со своими знаками передаточных отношений отдельных его ступеней, т.е.:

U_1n= (-1)^kU₁₂×U₂₃×U₃₄×…·U_(n-1)n. (4.19)

где k – число внешних зацеплений. Множитель (-1)^k позволяет определить знак передаточного отношения сложного зубчатого механизма.

Ступень передачи – контакт (зацепление) двух колес.

Рассмотрим определение передаточного отношения для различного типа соединений.

Пример 1. Рассчитать передаточное отношение от первого колеса к пятому (от ведущего к ведомому) U₁₄ для простого рядового соединения – зубчатые колеса расположены в один ряд (рисунок 4.23). Известны числа зубьев колес z₁, z₂, z₃ и z₄.

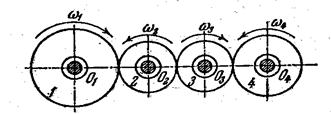
Рисунок 4.23 - Простое рядовое соединение

Решение. Количество ступеней (контактов) для данного соединения будет k =3. По формуле (4.19) имеем:

U₁₅ = (-1)³ U₁₂×U₂₃×U₃₄. (4.20)

Для каждой пары колес передаточное отношение определится по формуле (4.18), а именно:

U₁₂ = z₂/z₁, U₂₃ = z₃/z₂, U₃₄ = z₄/z₃.

Подставив эти значения в формулу (4.20), получим:

U₁₅ = (+).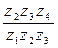

После сокращения, имеем:

U₁₄ = 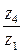. (4.21)

В формулу (4.21) не входят угловые скорости 2-го и 3-го колес. Зубчатые колеса, от которых не зависит величина передаточного отношения, называют паразитными колесами. В действительности паразитные колеса выполняют большую роль. От них зависит направление вращения ведомого вала. Их введение влияет на знак передаточного отношения. Они необходимы для передачи движения при большом межосевом расстоянии.

Пример 2. Рассчитать передаточное отношение ступенчатого соединения (рисунок 4.24).

Решение. Количество ступеней (контактов) для данного соединения будет k = 2. Представим передаточное отношение через произведение передаточных отношений каждой ступени (см. формулу 4.20):

U₁₄ = (-1)² U₁₂×U_2’3. (4.22)

Рисунок 4.24 - Кинематическая схема цилиндрического двухступенчатого редуктора

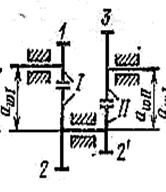
Число внешних зацеплений будет равно 2, поэтому знак передаточного отношения получится положительный. Через числа зубьев имеем:

U₁₃ = (+)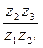. (4.23)

Таким образом, используя формулы (4.15), (4.18) и (4.19) можно рассчитать передаточное отношение любой передачи (не только зубчатой).

Дата добавления: 2014-01-20