Зацепление рабочего контура инструмента с нарезаемой заготовкой, осуществляемое в процессе нарезания по способу огибания, называется станочным зацеплением

Минимальное число зубьев зубчатого колеса, изготовленного без смещения и со смещением исходного контура

Согласно свойствам эвольвентного зацепления рабочий контур и эвольвентная часть профиля зуба нарезаемого колеса располагаются касательно друг к другу только на линии зацепления, начинающейся в точке А (рис. 10.5). Левее этой точки (в А₁) рабочий контур не касается эвольвентного профиля зуба колеса, а пересекает его. Это приводит к подрезанию зуба у его основания (рис. 10.4), а впадина между зубьями нарезаемого колеса получается более широкой. Подрезание уменьшает эвольвентную часть профиля зуба, что приводит к сокращению продолжительности зацепления каждой пары проектируемой передачи) и ослабляет зуб в опасном сечении. Поэтому подрезание не допустимо.

Рассмотрим различные положения заготовки колеса и рабочего контура (рис.10.5):

· 1 положение

Прямая вершин пересекает линию зацепления N-N в точке А₁, расположенной вне теоретической линии зацепления АВ.

· 2 положение

Прямая вершин проходит через крайнюю точку А линии зацепления.

· 3 положение

Отодвинем рабочий контур на величину xm. Прямая вершина пройдёт через точку А₂.

Построим эти положения рабочего контура на рис.10.5.

Во всех трёх случаях полюс зацепления Р при сдвиге рабочего контура не изменял своего положения

В первом положении зубья зубчатого колеса будут подрезаны.

Явление подрезов зубьев наблюдается в том случае, если рабочий участок линии зацепления аb выходит за пределы теоретического АВ.

Во втором положении случае зубья зубчатого колеса не будут подрезаны

При этом должно выполняться условие:

. (10.1)

Используя условие (10.1) определим минимальное число зубьев z колеса, при котором они не будут подрезаны. Из треугольника РАО следует, что

(10.2)

Из треугольника РА₂С₂ следует, что

(10.3)

Подставляя выражения (10.2) и (10.3) в условие (10.1) и решая его относительно z, получим:

(10.4)

Если х=0, то из выражения (10.4) найдем минимальное число зубьев колеса без смещения, которые не будут подрезаны режущим инструментом:

, (10 5)

Для стандартного зубчатого колеса при , a=20°, =17.

Для уменьшения габаритов зубчатых передач колеса следует проектировать с малым числом зубьев.

Поэтому при z<17, чтобы не произошло подрезания колеса должны быть изготовлены со смещением инструмента. Выясним, каково же минимальное смещение, при котором не получается подрезания зубьев. Оно определяется из условия (10.1)

Подставляя сюда значение из уравнения (10.5) и решая относительно х, запишем

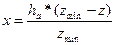. (10.6)

При h_a*=1 и z_min =17 получим

(10.7)

Формула (10.7) позволяет определять требуемую величину коэффициента смещения рабочего контура для нарезания желательного числа зубьев z без их подреза.

Дата добавления: 2014-01-20