И осевой силой винта

Теория винтовой пары

Зависимость между моментом, приложенным к гайке,

Если винт нагружен осевой силой Р (рис.2.11), то для завинчивания гайки к ключу необходимо приложить момент Т_к, а к стержню винта реактивный момент Т_р, который удерживает стержень от вращения.

Зависимость между Т_к и Р можно получить из уравнения работы:

А_к=А_т+А_р+А _p, (2.2)

где А_к - работа момента, приложенного к ключу; А_т – работа силы трения на опорном торце гайки; А_Р – работа силы трения в резьбе; А _p – работа силы Р на осевом перемещении.

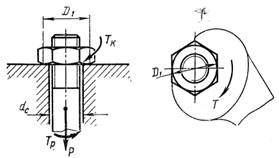Рис.2.11

Реактивный момент ТР в уравнении работы не участвует, так как стержень не вращается и работа этого момента равна нулю. Рассматривая один оборот гайки, получаем: Ак= Тк2p (2.3) Ат= Тт2p

Здесь Т_т – момент сил трения на опорном торце гайки (рис. 2.12,а).

Не допуская существенной погрешности, можно принять, что приведенный радиус сил трения на опорном торце гайки равен среднему радиусу этого торца или D_ср/2.

При этом

Т_т = Pf(D_ср/2), (2.4)

где D_ср = (D₁ + d_отв)/2; D_{1 –} наружный диаметр опорного торца гайки; d_отв – диаметр отверстия под винт; f – коэффициент трения.

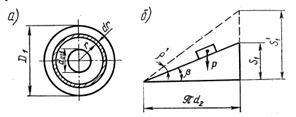
Сумму работ (А_р+А _p) за один оборот гайки можно определить, рассматривая движение груза Р по наклонной плоскости, угол которой равен углу подъема резьбы b (рис.2.12,б), а высота – ходу S_1.

Работа, затраченная на подъем груза по наклонной плоскости с учетом трения, равна работе подъема того же груза по некоторой фиктивной наклонной плоскости

Рис.2.12

без учета трения. При этом угол подъема фиктивной плоскости больше угла подъема действительной на угол трения.

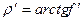
где f’ - приведенный коэффициент трения в резьбе – см. формулу (1.2)

Таким образом, получаем

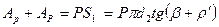(2.5)

Подставив выражения (2.3), (2.4) и (2.5) в формулу (2.2), после сокращения на 2p найдем искомую зависимость между Р и Т_к:

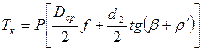(2.6)

Здесь первый член правой части есть момент сил трения на торце гайки Т_т - см. формулу (2.4), а второй член является моментом сил в резьбе

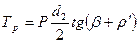(2.7)

Анализируя полученные зависимости, отметим:

1. По формуле (2.4) можно подсчитать отношение осевой силы винта Р к силе R, приложенной на ручке ключа.

2. Реактивный момент, необходимый для удержания стержня винта от проворачивания при завинчивании гайки, равен моменту сил в резьбе Т_р.

3. Стержень винта будет не только растягиваться силой Р, но и закручиваться моментом Т_Р (момент ключа Т_к не полностью передается стержню, так как часть его, равная Т_т, затрачивается на преодоление трения на торце гайки).

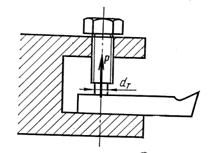Рис.2.13

4. Формула (2.4) для момента трения на торце гайки остается приближенно справедливой и для других подобных случаев. Например, величину момента трения на торце винта для зажима резца (рис.2.13) получим, приняв D1=dт и dотв = 0. При этом

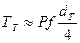
Дата добавления: 2014-01-20