Измерение информации. Человек получает информацию из окружающего мира с помощью органов чувств, анализирует ее и выявляет существенные закономерности с помощью мышления

Человек получает информацию из окружающего мира с помощью органов чувств, анализирует ее и выявляет существенные закономерности с помощью мышления, хранит полученную информацию в памяти. Процесс систематического научного познания окружающего мира приводит к накоплению информации в форме знаний (фактов, научных теорий и так далее). Таким образом, с точки зрения процесса познания информация может рассматриваться как знания.

Процесс познания можно наглядно изобразить в виде расширяющегося круга знания (такой способ придумали еще древние греки). Вне этого круга лежит область незнания, а окружность является границей между знанием и незнанием. Парадокс состоит в том, что чем большим объемом знаний обладает человек (чем шире круг знаний), тем больше он ощущает недостаток знаний (тем больше граница нашего незнания, мерой которого в этой модели является длина окружности) – рис. 1.1.

Рис. 1.1. Знание и незнание

Так, объем знаний выпускника школы гораздо больше, чем объем знаний первоклассника, однако и граница его незнания существенно больше. Действительно, первоклассник ничего не знает о законах физики и поэтому не осознает недостаточности своих знаний, тогда как выпускник школы при подготовке к экзаменам по физике может обнаружить, что существуют физические законы, которые он не знает или не понимает.

Само происхождение слова «информация» связано с сообщениями, сведениями, осведомлением. Такое значение слова «информация» продержалось довольно долго, примерно до середины нашего века. Именно в это время благодаря бурному развитию телеграфа, телефона, радио, телевидения и других средств массового общения и воздействия появилась необходимость измерять количество передаваемых сведений, т. е. информации. Начали возникать различные математические подходы к измерению информации, и это привело к тому, что первоначальное, зародившееся в глубине веков значение слова «информация» стало изменяться.

С появлением математических теорий понятие информации все чаще стало связываться с такой категорией, как вероятность. Наиболее четко эта связь была установлена и исследовала в работе американского математика и инженера К. Шеннона «Математическая теория связи», опубликованной в 1948 году.

Теория К. Шеннона называется вероятностно-статистической теорией информации. Именно в этой теории от первоначального недостаточно четкого представления об информации как о сведениях, которыми обмениваются люди, был совершен переход к точному понятию «количество информацин». Это понятие в статистической теории определялось на основе понятия «вероятности». Как известно, понятие «вероятность» всегда применяется для описания неопределенных ситуаций, когда эта неопределенность присуща или нашим знаниям об объекте или же самому этому объекту. Если сообщение не дает нам ничего нового, не снимает неопределенность, то с позиций рассматриваемой теории предполагается, что в нем не содержится информации. Так, например, для человека со средним образованием сообщение о том, что дважды два равно четырем, не содержит информации. Считается, что вероятность такого сообщения равна единице, а количество информации в нем равно нулю. Чем меньше вероятность тех или иных явлений {т. е., чем больше их сте пень неопределенности), тем большее количество информации содержится в сообщении об этих явлениях.

При таком подходе под информацией стали понимать лишь такие сведения, которые уменьшают существовавшую до их получения неопределенность. Информация здесь выступает как снимаемая неопределенность, как то, что уменьшает количество возможных вопросов, гипотез, предположений и т. д.

Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний. Если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно говорить, что такое сообщение содержит информацию.

Подход к информации как мере уменьшения неопределенности знаний позволяет количественно измерять информацию, что чрезвычайно важно для информатики.

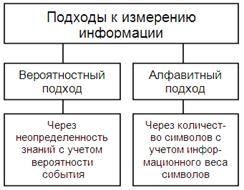
Рис. 1.2. Подходы к измерению информации

Вероятностный подход к измерению информации принят в теории информации и кодирования. Он исходит из следующей модели: получатель сообщения имеет определенное представление о возможных наступлениях некоторых событий. Эти события в общем случае недостоверны и выражаются вероятностями, с которыми получатель ожидает то или событие.

Базисным понятием всей теории информации является понятие энтропии. Энтропия в теории информации – мера хаотичности информации или мера внутренней неупорядоченности информации, связана с вероятностью появления тех или иных символов при передаче сообщений.

Количество информации в сообщении определяется тем, насколько уменьшилась эта мера после получения сообщения: чем больше энтропия системы, тем больше степень ее неопределенности. Поступающее сообщение полностью или частично снимает эту неопределенность. Основоположенник теории информации Клод Шеннон определил информацию, как снятую неопределенность. Точнее сказать, получение информации – необходимое условие для снятия неопределенности. Неопределенность возникает в ситуации выбора. Задача, которая решается в ходе снятия неопределенности – уменьшение количества рассматриваемых вариантов (уменьшение разнообразия), и в итоге выбор одного соответствующего ситуации варианта из числа возможных. Снятие неопределенности дает возможность принимать обоснованные решения и действовать. В этом управляющая роль информации.

Ситуация максимальной неопределенности предполагает наличие нескольких равновероятных альтернатив (вариантов), т.е. ни один из вариантов не является более предпочтительным. Причем, чем больше равновероятных вариантов наблюдается, тем больше неопределенность, тем сложнее сделать однозначный выбор и тем больше информации требуется для этого получить.

Минимальная неопределенность равна 0, т.е. эта ситуация полной определенности, означающая что выбор сделан, и вся необходимая информация получена.

Величина, характеризующая количество неопределенности в теории информации обозначается символом H и имеет название энтропия, точнее информационная энтропия.

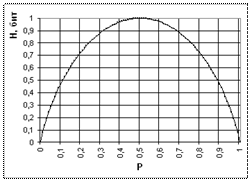
Рис. 1.3. Поведение энтропии для случая двух альтернатив

На рисунке 1.3 показано поведение энтропии для случая двух альтернатив, при изменении соотношения их вероятностей (p, (1-p)).

Максимального значения энтропия достигает в данном случае тогда, когда обе вероятности равны между собой и равны ½, нулевое значение энтропии соответствует случаям (p₀=0, p₁=1) и (p₀=1, p₁=0).

Количество информации I и энтропия H характеризуют одну и ту же ситуацию, но с качественно противоположенных сторон. I – это количество информации, которое требуется для снятия неопределенности H. Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H.

Впервые понятия «энтропия» и «информация» связал Клод Шеннон в 1948. С его подачи энтропия стала использоваться как мера полезной информации в процессах передачи сигналов по проводам. Следует подчеркнуть, что под информацией Шеннон понимал сигналы нужные, полезные для получателя. Неполезные сигналы, с точки зрения Шеннона, это шум, помехи. Если сигнал на выходе канала связи является точной копией сигнала на входе то, с точки зрения теории информации, это означает отсутствие энтропии. Отсутствие шума означает максимум информации. Взаимосвязь энтропии и информации нашло отражение в формуле:

H + Y = 1,

где Н – энтропия, Y – информация.

Для расчета энтропии Шеннон предложил уравнение, напоминающее классическое выражение энтропии, найденное Больцманом.

H = ∑P_i log₂ 1/P_i = -∑P_i log₂ Pi,

где Н – энтропия Шеннона, P_i - вероятность некоторого события.

Принято считать, что любая система стремится к состоянию равновесия, т. е. растет энтропия системы. Другими словами, энтропия максимальна в опытах, где все исходы равновероятны. Однако второе начало термодинамики требует компенсировать рост энтропии. Информация и является средством компенсации, т.к. при получении информации уменьшается неопределенность, то есть энтропия системы.

Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. С равной вероятностью произойдет одно из двух возможных событий – монета окажется в одном из двух положений: "орел" или "решка".

Возможные события		Произошедшее событие
Рис 1.4. Равновероятные события

Перед броском существует неопределенность наших знаний (возможны два события), и, как упадет монета, предсказать невозможно. После броска наступает полная определенность, так как мы видим (получаем зрительное сообщение), что монета в данный момент находится в определенном положении (например, "решка"). Это сообщение приводит к уменьшению неопределенности наших знаний в два раза, так как до броска мы имели два вероятных события, а после броска – только одно, то есть в два раза меньше.

В окружающей действительности достаточно часто встречаются ситуации, когда может произойти некоторое количество равновероятных событий. Так, при бросании равносторонней четырехгранной пирамиды существуют 4 равновероятных события, а при бросании шестигранного игрального кубика – 6 равновероятных событий.

Существует множество ситуаций, когда возможные события имеют различные вероятности реализации.

Например:

1. Когда сообщают прогноз погоды, то сведения о том, что будет дождь, более вероятно летом, а сообщение о снеге – зимой.

2. Если вы – лучший ученик в классе, то вероятность сообщения о том, что за контрольную работу вы получили 5, больше, чем вероятность получения двойки.

3. Если на озере живет 500 уток и 100 гусей, то вероятность подстрелить на охоте утку больше, чем вероятность подстрелить гуся.

4. Если в мешке лежат 10 белых шаров и 3 черных, то вероятность достать черный шар меньше, чем вероятность вытаскивания белого.

5. Если монета несимметрична (одна сторона тяжелее другой), то при ее бросании вероятности выпадения “орла” и “решки” будут различаться.

Чем больше количество возможных событий, тем больше начальная неопределенность и, соответственно, тем большее количество информации будет содержать сообщение о результатах опыта.

Информацию можно рассматривать как набор сообщений. Сообщение – это форма представления каких либо сведений в виде речи, текста, изображений, цифровых данных, графиков, таблиц и т.п.

Сообщение, в свою очередь, состоит в возможности наступления некоторых событий, каждое из которых может иметь свою вероятностную характеристику, т.е. степень возможности наступления этого события.

Пример 1. В закрытом ящике лежат два шара – черный и белый. Вытаскиваем один шар. Перед вытаскиванием существовала неопределенность нашего знания, так как возможны два события: «вытащили черный шар» или «вытащили белый шар». После того, как шар вытащен, наступает полная определенность: если произошло событие «вытащили черный шар», то в ящике остался белый и наоборот.

Вытаскивание одного из двух шаров приводит к уменьшению неопределенности нашего знания в два раза.

Рассмотрим понятие «вероятность».

Если N – это общее число возможных исходов какого-то процесса (например, вытаскивание шара), а из них интересующее нас событие (например, вытаскивание белого шара) может произойти k раз, то вероятность этого события p можно определить по формуле:

p = k/N.

Вероятность выражается в долях единицы. В нашем примере вероятность вытаскивания как белого, так и черного шара равна ½, т.е. события равновероятны.

Вероятность достоверного события (из 50 белых шаров вытащили белый шар) равна 1; вероятность невозможного события (из 50 белых шаров вытащили черный шар) равна 0.

Пример 2. В закрытом ящике лежат четыре шара – три черных и один белый. Вытаскиваем один шар. Его цвет, скорее всего, будет черным. Но может быть быть и белым. Посчитаем вероятность вытаскивания белого и черного шара:

p_{бел .} = ¼ = 0,25; p_черн. = ¾ = 0,75.

Информация содержится в сообщении о цвете вытащенного шара. Какая информация в примере 2 ценнее: «вытащили белый шар» или «вытащили черный шар? Конечно, информация о том, что вытащили белый шар, т.е. этим сообщением получено полное знание, что в ящике остались только черные шары.

Информация о том, что вытащили черный шар, тоже уменьшает неопределенность знания (после этого события в ящике осталось три шара – один белый и два черных), но не дает полного знания, какой шар может быть вытащен следующим.

Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.

Количественная зависимость между вероятностью события p и количеством информации в сообщении о нем i выражается формулой

i = log₂(1/ p) (1)

или

2 ⁱ = 1/ p (2)

(Напомним, что такое логарифм.

Нахождение логарифма b по основанию a – это нахождение степени, в которую нужно возвести a, чтобы получить b.

Логарифм по основанию 2 называется двоичным:

log₂(8)=3, т.к. 2³=8

log₂(10)=3,32, т.к. 2^3,32=10

Логарифм по основанию 10 называется десятичным:

log₁₀(100)=2, т.к. 10²=100)

Если событие достоверно, его вероятность равна 1, то оно неинформативно, т.е. количество информации в сообщении о нем равно 0. Но чем меньше вероятность какого-то события, тем большую ценность имеет информация об этом событии и тем больше будет значение i.

Например, куратор сообщил вам, что как обычно после этого занятия будет перерыв. (Так как вероятность этого события велика, то количество информации в нем мало.)

Куратор сообщил вам, что в перерыве будут бесплатно раздавать апельсины, бананы, ананасы. (Так как данное событие маловероятно, то количество информации в нем для вас велико.)

Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений.

Для количественного выражения любой величины необходимо определить единицу измерения. Например, для измерения длины выбран определенный эталон метр, массы – килограмм.

За единицу измерения количества информации принимается такое количество информации, которое содержится в сообщении, уменьшающем неопределенность знания в 2 раза. Такая единица называется « бит» (от английского словосочетания «BI nary digi T» – «двоичная цифра»).

Вернемся к рассмотренному выше получению информационного сообщения о том, что выпал «орел» при бросании монеты. Здесь неопределенность уменьшилась в 2 раза, следовательно, это сообщение равно 1 биту. Сообщение о том, что выпала определенная грань игрального кубика, уменьшает неопределенность в 6 раз, следовательно, это сообщение равно 6 битам.

Минимальной единицей измерения количества информации является бит, а следующей по величине единицей – байт, причем

1 байт = 8 бит

В международной системе СИ используют десятичные приставки «Кило» (10³), «Мега» (10⁶), «Гига» (10⁹),… В компьютере информация кодируется с помощью двоичной знаковой системы, поэтому в кратных единицах измерения количества информации используется коэффициент 2ⁿ.

1 килобайт (Кб) = 2¹⁰ байт = 1024 байт

1 мегабайт (Мб) = 2¹⁰ Кбайт = 1024 Кб

1 гигабайт (Гб) = 2¹⁰ Мбайт = 1024 Мб

1 терабайт (Тб) = 2¹⁰ Гбайт = 1024 Гб

Терабайт – очень крупная единица измерения информации, поэтому применяется крайне редко. Всю информацию, которое накопило человечество, оценивают в десятки терабайт.

Существует формула, которая связывает между собой количество возможных информационных сообщений N и количество информации i, которое несет полученное сообщение:

N=2ⁱ (3)

По этой формуле можно легко определить количество возможных событий, если известно количество информации. Например, если известно, что в результате определения того, что интересующий нас Коля Иванов живет на втором этаже, было получено 3 бит информации, то количество этажей в доме можно определить как N=2³=8 этажей.

Если же вопрос стоит так: «в доме 8 этажей, какое количество информации мы получили, узнав, что интересующий нас Коля Иванов живет на втором этаже?», нужно воспользоваться формулой: i=log₂(8)=3 бит.

Пример 3. Игра «Угадай число»

На примере игры "Угадай число" можно рассмотреть уменьшение неопределенности. Один из участников загадывает целое число (например, 30) из заданного интервала (например, от 1 до 32), цель второго - "угадать" число первого участника. Для второго игрока начальная неопределенность знания составляет 32 возможных события. Чтобы найти число, необходимо получить определенное количество информации. Первый участник может отвечать только "да" и "нет". Второй должен выбрать следующую стратегию: последовательно, на каждом шаге уменьшать неопределенность знания в два раза. Для этого он должен делить числовой интервал пополам, задавая свои вопросы.

Вопрос второго	Ответ первого	Количество возможных событий (неопределенность знаний)	Полученное количество информации
Число больше 16?	Да		1 бит
Число больше 24?	Да		1 бит
Число больше 28?	Да		1 бит
Число больше 30?	Нет		1 бит
Число 30?	Да		1 бит

Для того чтобы угадать число из интервала от 1 до 32 потребовалось 5 вопросов. Количество информации, необходимое для определения одного из 32 чисел, составило 5 бит.

Таким образом, очень приближенно можно сказать, что количество информации в сообщении о каком-то событии совпадает с количеством вопросов, которые необходимо задать, чтобы получить ту же информацию, ответ на эти вопросы может быть лишь "да" или "нет".

Вернемся к примеру 1.

Пусть x – количество информации в сообщении о том, что вытащен белый шар. Тогда

2 ^x = 1/0,5 Þ 2 ^x = 2 Þ x = 1 бит,

т.е. мы доказали, что сообщение об одном событии из двух равновероятных несет 1 бит информации.

Количество информации можно рассчитать методами Р. Хартли и К. Шеннона.

Американский инженер Р. Хартли в 1928 г. процесс получения информациирассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N. I =log₂N. Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log₂100 = 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации. Определим теперь, являются ли равновероятными сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина". Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины. Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе. Формула Шеннона: I = – (p₁log₂p₁ + p₂log₂p₂ +... + _pNlog2pN), где p_i — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений. Легко заметить, что если вероятности p₁,..., p_N равны, то каждая из них равна 1/N и формула Шеннона превращается в формулу Хартли.

Пример 4. В мешке лежат 64 монеты. Сообщение о том, что достали золотую монету, несет 4 бит информации. Сколько золотых монет было в мешке?

Дано: N = 64; i _зол. = 4.

Найти k _зол.

Сообщение о том, что достали золоту монету. несет 4 бит информации. Следовательно:

2⁴ = 1/ p _зол.

Отсюда можно найти вероятность вытаскивания золотой монеты:

p_зол. = 1/16.

С другой стороны, p _зол. = k _зол./ N, следовательно, k _зол.= Np _зол. = 84/16 = 4.

Ответ: Число золотых монет – 4.

Пример 5. В ящике лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар?

Дано: k _черн. = 8; k _бел. = 24.

Найти: i _черн.

N = k _черн. + k _бел. = 32;

p = k_черн./N = 8/32 = ¼;

2 ⁱ_черн. = 1/p _черн. = 4;

i_черн. = 2 бит.

Ответ: сообщение о том, что достали черный шар, несет 2 бит информации.

В примерах 1-5 количество возможных вариантов информации являлось целой степенью числа 2. Если же количество возможных вариантов информации не является целой степенью числа 2, то необходимо воспользоваться калькулятором или следующей таблицей, в которой N – общее количество равновероятных событий; i – количество информации, бит.

Таблица 1.1

Количество информации в сообщении об одном из N равновероятных событий:

N	i	N	i	N	i	N	i
	0,00000		4,08746		5,04439		5,61471
	1,00000		4,16993		5,08746		5,64386
	1,58496		4,24793		5,12928		5,67243
	2,00000		4,32193		5,16993		5,70044
	2,32193		4,39232		5,20945		5,72792
	2,58496		4,45943		5,24793		5,75489
	2,80735		4,52356		5,28540		5,78136
	3,00000		4,58496		5,32193		5,80735
	3,16993		4,64386		5,35755		5,83289
	3,32193		4,70044		5,39232		5,85798
	3,45943		4,75489		5,42626		5,88264
	3,58496		4.80735		5,45943		5.90689
	3,70044		4,85798		5,49185		5,93074
	3,80735		4,90689		5,52356		5,95420
	3,90689		4,95420		5,55459		5,97728
	4,00000		5,00000		5,58496		6,00000

Пример 6. При игре в кости используется кубик с шестью гранями. Сколько бит информации получает игрок при каждом бросании кубика?

Выпадение каждой грани кубика равновероятно и равно 1/6. Поэтому количество информации от каждого броска находится из уравнения 2 ⁱ = 6. Решая это уравнение по формуле (1): i = log₂6, получаем ответ: i = 2.585 бит. Решение примера 5 можно получить, воспользовавшись таблицей 1, в которой N – общее количество равновероятных событий; i – количество информации, бит.

Оценка информации, так же как вещества или энергии, может быть субъективной и объективной. В первом случае главное – смысл информации, а во втором – её измеримость.

Первый способ измерения информации отражает вероятностный (содержательный) подход. Этот метод является субъективным.

Алфавитный подход к измерению информации позволяет определить количество информации, заключенной в тексте. Алфавитный подход является объективным, т.е. он не зависит от субъекта (человека), воспринимающего текст.

Множество символов, используемых при записи текста, называется алфавитом. Полное количество символов в алфавите называется мощностью (размером) алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из русских букв и дополнительных символов равна 54. Чем большее количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак.

С помощью формулы (3) определим количество информации, которое несет один символ русского алфавита:

N = 54 => Используя таблицу 1.1, получаем i = 5,755 бит.

Вот сколько информации несет один символ в русском тексте! А теперь для того, чтобы найти количество информации во всем тексте, нужно посчитать число символов в нем и умножить на i.

Возьмем с книжной полки какую-нибудь книгу и посчитаем количество информации на одной ее странице. Пусть страница содержит 50 строк. В каждой строке — 60 символов. Значит, на странице умещается 50*60 = 3000 знаков. Тогда объем информации будет равен: 5,755 х 3000 = 17265 бит.

Следовательно, при алфавитном подходе к измерению информации количество информации от содержания не зависит. Количество информации зависит от объема текста (то есть от числа знаков в тексте) и от мощности алфавита.

Отсюда следует, например, что нельзя сравнивать информационные объемы текстов, написанных на разных языках, только по объему. У них отличаются информационные веса одного символа, так как мощности алфавитов разных языков - различные.

Но если книги написаны на одном языке, то понятно, что в толстой книге информации больше, чем в тонкой. При этом содержательная сторона книги в расчет не берется.

Вероятностный подход применим и для алфавитного подхода к измерению информации, заключенной в тексте. Известно, что разные символы (буквы алфавита, знаки препинания и др.) встречаются в тексте с разной частотой и, следовательно, ммеют разную вероятность. Например, в русской письменной речи в среднем на 1000 знаков осмысленного текста приходится 200 букв "а" и в сто раз меньшее количество буквы "ф" (всего 2). Таким образом, с точки зрения теории информации, информационная емкость знаков русского алфавита различна (у буквы "а" она наименьшая, а у буквы "ф" - наибольшая).Значит, измерять информационный вес каждого символа в тексте в предположении равновероятности нельзя.

Пример 7. В алфавите 4 буквы (А, В, С, D), один знак препинания «.» и один разделитель (пробел). В тексте 10000 знаков, из них:

A – 4000

B – 1000

C – 2000

D – 1500

точек – 500

пробелов – 1000.

Какой объем информации в тексте?

Если считать, что частотный алфавит определен для любого текста на этом языке, то можно найти вероятность каждого символа текста и информационный вес:

A: 4000/10000 = 0,4; i_A = log₂(1/0,4) = 1,32;

B: 1000/10000 = 0,1; i_B = log₂(1/0,1) = 3,19;

C: 2000/10000 = 0,2; i_C = log₂(1/0,2) = 2,32;

D: 1500/10000 = 0,15; i_D = log₂(1/0,15) = 2,73;

точка: 500/10000 = 0,05; i_точка = log₂(1/0,05) = 4,32;

пробел: 1000/10000 = 0,1; i_пробел = log₂(1/0,1) = 3,19.

Общий объем информации в тексте вычислим по формуле суммы произведений информационного веса каждого символа на число повторений этого символа:

I = i_A*n_A + i_B*n_B + i_C*n_C + i_D*n_D + i_точка* n_точка + i_пробел* n_пробел =

1,32 * 4000 + 3,19 * 1000 + 2,32 * 2000 + 2,73 * 1500 + 4,32 * 500 + 3,19 * 1000 = 22841,84 бит.

Дата добавления: 2014-01-20