Площадь криволинейной трапеции. Понятие определённого интеграла

ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

Понятие определённого интеграла

Пусть вы имеете:

1) отрезок на оси

2) функцию 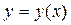однозначную, неотрицательную и непрерывную на .

По этим данным строим фигуру называемую криволинейной трапецией, прилегающей сверху к оси (рис. 13.1).

Рис. 1.1 Рис. 1.2 Рис. 1.3

Как найти площадь фигуры Можно мысленно разбить на бесконечно узкие вертикальные кусочки (рис. 1.2). Сложив (просуммировав) их площади, получим площадь всей фигуры. Сложение (суммирование) бесконечно большого количества бесконечно малых величин и есть интегрирование.

Рассмотрим кусочек бесконечно малой ширины (рис. 1.3). Из-за малости высота кусочка не успевает заметно измениться, поэтому кусочек считаем прямоугольником высотой площадь которого равна

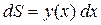или просто

Площадь всей фигуры равна сумме (интегралу) площадей таких прямоугольников и обозначается так:

(1.1)

Итак, если то

Далее будем рассматривать функцию которая может быть как положительной, так и отрицательной.

Числа 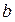– это нижний и верхний пределы интегрирования,

отрезок – область (отрезок) интегрирования,

подынтегральная функция,

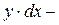подынтегральное выражение,

переменная интегрирования, изменяющаяся от до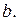

Запишем ещё раз формулу (1.1), справедливую при :

Площадь фигуры, ограниченной графиком функции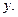

Геометрический смысл определённого интеграла

(1.2)

Посмотрите на рис. 1.1. Если точку приближать к точке площадь будет уменьшаться и при станет Поэтому

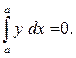
(1.3)

Если на интервале (рис. 1.4), будем иметь прямоугольник, площадь которого равна и по формуле (1.2) получим

(1.4)

Пример: Рис. 1.4

Если фигура 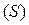будет прилегать снизу к оси (рис. 1.5). В этом случае поэтому Значит,

Если	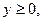Если
то	то

(1.5)

Итак, каков знак у подынтегральной функции, таков знак и у интеграла.

Если функция попеременно меняет знак (рис. 1.6), то

.

Рис. 1.5 Рис. 1.6

Всякий ли определённый интеграл существует, т. е. равен какому-либо числу? Оказывается, что если область интегрирования и подынтегральная функция конечны, то определённый интеграл всегда существует.

Тренировка по теме

«Площадь криволинейной трапеции. Понятие криволинейного интеграла»

Запишите с помощью определённого интеграла площадь фигуры, ограниченной следующими линиями:

а) осями координат, прямой и параболой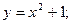

1) 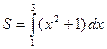2) 3) 4)

5)

б) осью абсцисс, прямыми 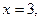и линией

1) 2) 3) 4)

5)

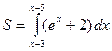
Дата добавления: 2014-01-20