Тройные интегралы

ЛЕКЦИЯ 3

Тройные интегралы. Вычисление тройных интегралов в декартовой системе координат. Замена переменных в кратных интегралах Вычисление тройных интегралов в цилиндрической и сферической системах координат.

2.1. Вычисление тройных интегралов в
декартовой системе координат

По аналогии с двойным интегралом вводится понятие тройного интеграла. Пусть в некоторой замкнутой ограниченной области T трехмерного пространства задана ограниченная функция трех переменных f (x,y,z). Разобьем эту область на n произвольных частей с объемами D v_i. В каждой частичной области возьмем произвольную точку M (x_i,y_i,z_i) и составим сумму:

,

которая называется интегральной суммой для функции f(x,y,z) по области T. Если интегральная сумма при n ®¥ (при этом диаметры всех областей должны стремится к нулю: 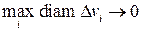) имеет предел, то этот предел называется тройным интегралом:

. (2.1)

Отметим, что тройные интегралы обладают свойствами, аналогичные свойствам двойных интегралов.

Перейдем теперь к вопросу о вычислении тройных интегралов в декартовой системе координат. Предположим, что область T является простой в направлении оси Oz, т.е. любая прямая, проведенная параллельно оси Oz, пересекает границу области T не более чем в двух точках. Это означает, что область T ограничена снизу поверхностью z=z ₁(x,y), сверху поверхностью z=z ₂(x,y) и с боков – цилиндрической поверхностью с образующими, параллельными оси Oz. Тогда по аналогии с формулой вычисления объемов цилиндрических тел при помощи двойных интегралов, можно получить

. (2.2)

Здесь D проекция области T на плоскость xOy. Если область D является простой в направлении оси Oy, то можно написать

. (2.3)

Отметим, что здесь внешний интеграл обязательно (!) должен иметь постоянные пределы (т.е. числа), пределы во втором интеграле могут зависеть только от той переменной, которая стоит во внешнем интеграле.

Если в тройном интеграле подынтегральная функция f(x,y,z)º1, то тройной интеграл будет равен объему области интегрирования T, т.е.

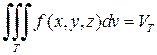. (2.4)

При вычислении тройных интегралов следует: 1) сделать чертеж области интегрирования T; 2) изобразить проекцию области T на выбранную координатную плоскость; 3) расставить пределы интегрирования.

Пример 2.1. Вычислить

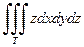, если

Решение. Область T ограничена сверху плоскостью , отсекающей на координатных осях отрезки 6, 4 и 2, соответственно; снизу область T ограниченна плоскостью z =0, т.е. координатной плоскостью xOy. Проекцией области T на плоскость xOy служит треугольник, образованный прямыми x =0, y =0 и 2 x +3 y =12. В результате получаем

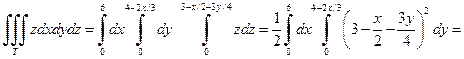
Пример 2.2. Вычислить объем тела, ограниченного поверхностями z =2 x ²+ y ²+1, x+y =1, x =0, y =0, z =0.

Решение. Сделаем чертеж. z= 2 x ²+ y ²+1 – это параболоид с главной осью, параллельной оси Oz; x+y =1 – это плоскость, параллельная оси Oz и отсекающая на осях Ox и Oy отрезки, равные 1; x =0, y =0, z =0 – это координатные плоскости. Данное тело проектируется на плоскость xOy в виде треугольника. Расставим пределы интегрирования:

.

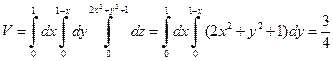Дата добавления: 2014-01-20