
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
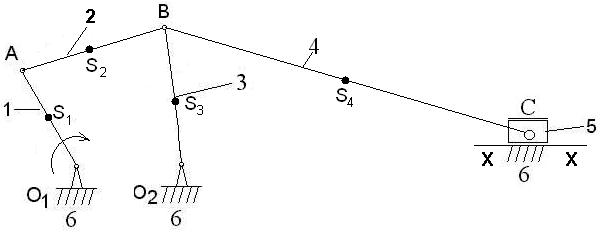
Решение. Определение ускорений точек звеньев и угловых ускорений звеньев для заданного положения механизма
|
|
|
|
Определение ускорений точек звеньев и угловых ускорений звеньев для заданного положения механизма.
Пример 4. 2.
1.Определение ускорения точки А.
Так как угловая скорость  является постоянной, то
является постоянной, то  .
.
 . Вектор ускорения
. Вектор ускорения 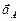 направлен параллельно кривошипу О1 А от точки А к точке О1.
направлен параллельно кривошипу О1 А от точки А к точке О1.
Выбираем масштаб плана ускорений 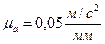 . Найдём отрезок, изображающий вектор ускорения
. Найдём отрезок, изображающий вектор ускорения 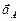 на плане:
на плане: 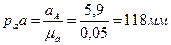 . Из полюса плана ускорений
. Из полюса плана ускорений  откладываем данный отрезок в направлении, параллельном АО1.
откладываем данный отрезок в направлении, параллельном АО1.
2.Определение ускорения точки В.
Запишем векторное уравнение: 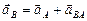 .
.
Вектор относительного ускорения 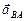 раскладываем на нормальную и касательную составляющие:
раскладываем на нормальную и касательную составляющие: 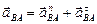 .
.
Нормальное относительное ускорение равно: 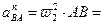
 .
.
Найдём отрезок, изображающий вектор ускорения 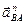 на плане:
на плане: 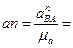
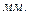
Продолжаем строить план ускорений. Вектор ускорения 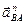 направлен параллельно АВ. Откладываем отрезок
направлен параллельно АВ. Откладываем отрезок 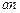 из точки
из точки 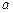 плана ускорений в указанном направлении от точки В к точке А.
плана ускорений в указанном направлении от точки В к точке А.
Вектор ускорения 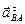 направлен перпендикулярно АВ. Проводим это направление из точки
направлен перпендикулярно АВ. Проводим это направление из точки 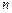 плана ускорений.
плана ускорений.
План ускорений 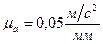
Вектор ускорения  раскладываем на нормальную и касательную составляющие:
раскладываем на нормальную и касательную составляющие:
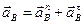 .
.
Нормальное ускорение равно: 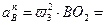
 .
.
Найдём отрезок, изображающий вектор ускорения 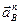 на плане:
на плане: 
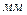 .
.
Продолжаем строить план ускорений. Вектор ускорения 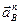 направлен параллельно ВO2. Откладываем отрезок
направлен параллельно ВO2. Откладываем отрезок 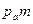 из точки
из точки  плана ускорений в указанном направлении от точки В к точке O2. Вектор ускорения
плана ускорений в указанном направлении от точки В к точке O2. Вектор ускорения  направлен перпендикулярно ВO2. Проводим это направление из точки m плана ускорений. Две прямые линии, проведённые из точек
направлен перпендикулярно ВO2. Проводим это направление из точки m плана ускорений. Две прямые линии, проведённые из точек  и
и 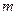 в указанных направлениях, пересекаются в точке
в указанных направлениях, пересекаются в точке 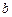 .
.
Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб  , получим:
, получим:
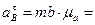
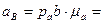
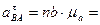
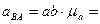
3.Определение ускорения точки C.
Запишем векторное уравнение: 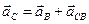 .
.
Вектор относительного ускорения 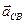 раскладываем на нормальную и касательную составляющие:
раскладываем на нормальную и касательную составляющие: 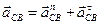 .
.
Нормальное относительное ускорение равно: 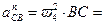
 .
.
Найдём отрезок, изображающий вектор ускорения 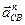 на плане:
на плане: 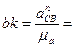
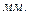
Продолжаем строить план ускорений. Так как отрезок 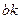 мал, то его на плане ускорений не откладываем. Точки
мал, то его на плане ускорений не откладываем. Точки 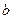 и
и 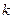 совпадают.
совпадают.
Вектор ускорения 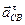 направлен перпендикулярно ВС. Проводим это направление из точки
направлен перпендикулярно ВС. Проводим это направление из точки 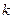 плана ускорений.
плана ускорений.
Вектор ускорения 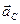 направлен параллельно оси x – x. Проводим это направление из полюса
направлен параллельно оси x – x. Проводим это направление из полюса  . Две прямые линии, проведённые из точек
. Две прямые линии, проведённые из точек 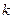 и
и  в указанных направлениях, пересекаются в точке
в указанных направлениях, пересекаются в точке  .
.
Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб  , получим:
, получим:
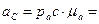
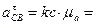

4.Определение ускорения точки 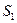 .
.
 . Вектор ускорения
. Вектор ускорения  направлен параллельно кривошипу О1 А от точки S1 к точке О1.
направлен параллельно кривошипу О1 А от точки S1 к точке О1.
5.Определение ускорения точки 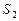 .
.
Воспользуемся следствием из теоремы подобия. Составим пропорцию:
 ,
, 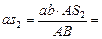
Данный отрезок откладываем на прямой 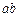 от точки
от точки 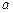 . Точку
. Точку 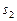 соединяем с полюсом
соединяем с полюсом  .
.
Величина ускорения: 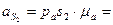
6.Определение ускорения точки  .
.
Воспользуемся следствием из теоремы подобия. Составим пропорцию:
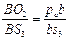 ,
, 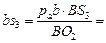
Данный отрезок откладываем на прямой 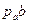 от точки
от точки 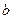 . Точку
. Точку 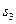 соединяем с полюсом
соединяем с полюсом  .
.
Величина ускорения: 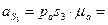
7.Определение ускорения точки 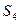 .
.
Воспользуемся следствием из теоремы подобия. Составим пропорцию:
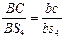 ,
, 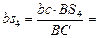
Данный отрезок откладываем на прямой 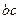 от точки
от точки 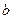 . Точку
. Точку  соединяем с полюсом
соединяем с полюсом  .
.
Величина ускорения: 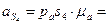
8.Определение углового ускорения шатуна АВ.
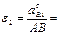
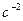 . Для определения направления
. Для определения направления 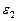 переносим вектор
переносим вектор 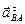 в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует
в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует 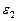 . В данном случае угловое ускорение
. В данном случае угловое ускорение 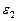 направлено против часовой стрелки.
направлено против часовой стрелки.
9.Определение углового ускорения коромысла ВO2.
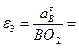
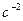 . Для определения направления
. Для определения направления 
 переносим вектор
переносим вектор  в точку В коромысла ВО2 и смотрим как она движется относительно точки О2. Направление этого движения соответствует
в точку В коромысла ВО2 и смотрим как она движется относительно точки О2. Направление этого движения соответствует  . В данном случае угловое ускорение
. В данном случае угловое ускорение  направлено по часовой стрелке.
направлено по часовой стрелке.
10.Определение углового ускорения шатуна ВС.
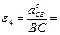
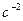 . Для определения направления
. Для определения направления 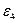 переносим вектор
переносим вектор 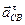 в точку C шатуна ВС и смотрим как она движется относительно точки B. Направление этого движения соответствует В данном случае угловое ускорение
в точку C шатуна ВС и смотрим как она движется относительно точки B. Направление этого движения соответствует В данном случае угловое ускорение 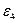 направлено против часовой стрелки.
направлено против часовой стрелки.
| Исследуемая величина | Отрезок на плане | Направление | Величина отрезка на плане, 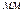
| Масштабный коэффициент

| Значение величины, 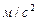
|
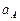
| 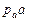
| 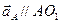
| 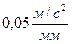
| ||

| 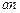
| 
| |||
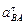
| 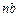
| 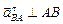
| |||
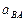
| 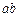
| 
| |||

| 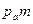
| 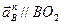
| |||
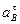
| 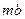
| 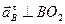
| |||

| 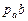
| ||||
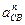
| 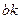
| 
| |||

| 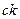
| 
| |||
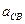
| 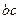
| ||||
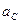
| 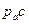
| 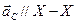
| |||
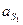
| 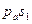
| 
| |||
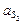
| 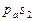
| ||||
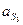
| 
| ||||

| 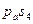
| ||||
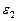
| |||||

| |||||
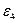
|
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 655; Нарушение авторских прав?; Мы поможем в написании вашей работы!