Уравнение Бернулли для относительного движения

Представляет интерес другой вывод уравнения Л.Эйлера, позволяющий несколько глубже понять механизм преобразования энергии рабочим колесом турбины, а именно вывод, основанный на уравнении Бернулли.

Однако в данном случае нужно использовать уравнение Бернулли, записанное для относительного движения w.

Представим себе что имеется диск, вращающийся с частотой n, (об/мин), на высоте z над плоскостью сравнения 0 – 0, рисунок 4.11. На диске укреплена трубка 1 – 2. По трубке от сечения 1 к сечению 2 движется жидкость с относительной скоростью w (относительно трубки).

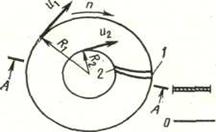
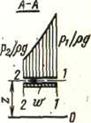
Рисунок 4.11. К уравнению Бернулли для относительного движения

В данном случае уравнение Бернулли для плоскости сравнения 0-0 имеет вид:

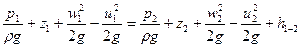(1)

Здесь h_{1 - 2} — потери напора на участке 1 – 2; u₁ и u₂ — окружные скорости (переносные).

Особенность состоит в том, что в рассматриваемых условиях удельная энергия жидкости при движении вдоль трубки может убывать или возрастать в зависи­мости от изменения переносной скорости u₁ и u₂. Это свойство и используется в рабочем колесе турбины, каналы которого, образованные лопастями, представ­ляют собой систему «трубок».

Из этого уравнения следует, что:

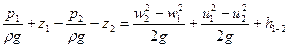(2)

Удельная энергия жидкости при входе на рабочее колесо:

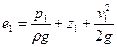
Удельная энергия жидкости при сходе с рабочего колеса:

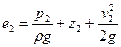
Разность удельных энергий:

e₁ – e₂ =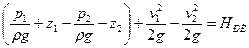

Заменив выражение в скобках на выражение правой части (2), получим:

Н_Р.К. =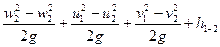

Записав Н_Р.К. – h_1-2 = H·η_Г, приходим к еще одной форме уравнения Эйлера:

Н_Р.К. =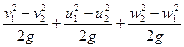

которая особенно ясно показывает прямую зависимость H·η_Г от треугольников ско­ростей на входе и выходе рабочего колеса.

Это выражение основного уравнения турбины объясняет связь формы рабочего колеса с напором турбины. В осевых турбинах u₁ = u₂ и, следовательно, H·η_Г определяется только абсолютными и отно­сительными скоростями, которые не могут быть слишком большими, так как иначе возрастут потери. Это и вызывает ограничение использо­вания осевых турбин по напору. С ростом Н переходят на диагональные и радиально-осевые турбины, у которых действует и различие пе­реносных скоростей u₁ и u₂, причем чем больше Н, тем роль этого фактора возрастает. Этим объясняется то, что у высоконапорных тур­бин увеличивается отношение D₁ / D₂ (см. рисунок 7.3).

Дата добавления: 2014-01-20