
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Криволинейный интеграл
|
|
|
|
При решении некоторых задач механики и физики возникают интегральные суммы, отличные по своему виду от определенного и кратного интегралов. Например, при вычислении работы, произведенной переменной силой  , кривую
, кривую 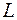 , по которой движется материальная точка, разбивают точками
, по которой движется материальная точка, разбивают точками 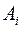 на достаточно малые дуги
на достаточно малые дуги 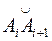 такие, что в пределах каждой из них силу принимают постоянной и равной
такие, что в пределах каждой из них силу принимают постоянной и равной  , а перемещение материальной точки приближенно считают прямолинейным. Тогда работу силы на каждом участке вычисляют по известной формуле
, а перемещение материальной точки приближенно считают прямолинейным. Тогда работу силы на каждом участке вычисляют по известной формуле 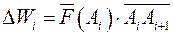 (скалярное произведение векторов), точное значение работы по всей дуге кривой
(скалярное произведение векторов), точное значение работы по всей дуге кривой 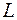 равно пределу суммы работ
равно пределу суммы работ 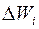 при неограниченном возрастании дробности деления дуги кривой
при неограниченном возрастании дробности деления дуги кривой 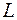
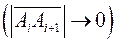 . Предел указанной суммы для произвольной функции
. Предел указанной суммы для произвольной функции  получил название криволинейного интеграла (криволинейного интеграла 2-го рода).
получил название криволинейного интеграла (криволинейного интеграла 2-го рода).
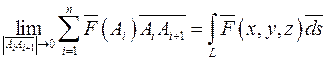 .
.
Если использовать координатную форму записи скалярного произведения векторов  и
и 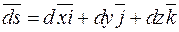 , то криволинейный интеграл можно записать в виде
, то криволинейный интеграл можно записать в виде
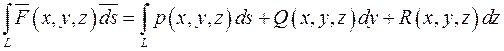 .
.
Для плоской кривой 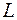 криволинейный интеграл записывается в виде
криволинейный интеграл записывается в виде
 .
.
Определенный интеграл является частным случаем криволинейного, когда путь интегрирования 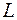 есть прямая
есть прямая  .
.
Свойства криволинейного интеграла:
1. При изменении направления обхода пути интегрирования знак интеграла меняется на противоположный
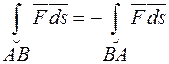 .
.
2. Свойство суперпозиции (работа силы равна сумме работ составляющих)
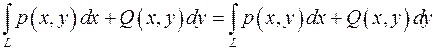 .
.
3. Если кривая интегрирования состоит из двух дуг 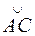 и
и 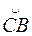 , то
, то
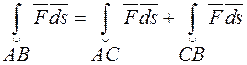 .
.
Другие свойства совпадают со свойствами определенного интеграла.
Если Кривая 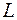 задана уравнением
задана уравнением  , то вычисление криволинейного интеграла производится по формуле
, то вычисление криволинейного интеграла производится по формуле
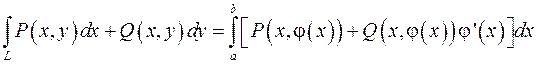 ,
,
где 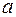 и
и 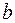 – пределы изменения координат точек кривой.
– пределы изменения координат точек кривой.
В случае кривой 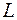 , заданной параметрическими уравнениями:
, заданной параметрическими уравнениями:  ,
, 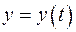 ,
, 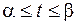 a для вычисления криволинейного интеграла применяют формулу
a для вычисления криволинейного интеграла применяют формулу
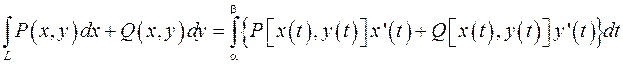 .
.
При вычислении интеграла по замкнутой кривой ее разбивают на несколько дуг. Если путь интегрирования L есть замкнутая кривая без самопересечений, то интегрирование производится в направлении против часовой стрелки. При интегрировании по замкнутой кривой часто удобно использовать параметрические уравнения данной кривой.
Пример.
Вычислить 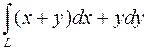 по окружности радиуса 1 с центром в начале координат (см. рис.18)
по окружности радиуса 1 с центром в начале координат (см. рис.18)
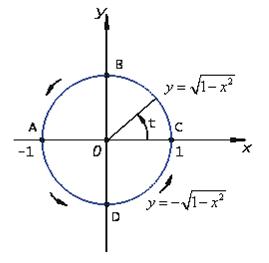
Рис. 18
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 487; Нарушение авторских прав?; Мы поможем в написании вашей работы!