Пример 2. Установление тока при замыкании цепи

В момент 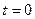быстро повернем ключ К против часовой стрелки из верхнего положения в нижнее (рис. 3.5, б). Этим самым мы подключили к индуктивности L источник 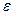. Ток в цепи начнет нарастать и опятьвозникает ЭДС самоиндукции, противодействующая этому нарастанию. Согласно закону Ома 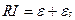. или

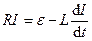
Перенесем 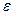в левую часть уравнения и введем новую переменную 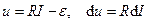. После этого полученное уравнение преобразуем к виду

,

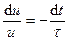где 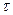= L/R – постоянная времени.

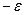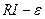Интегрирование по и (от до ) и 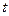(от 0 до )

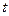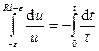
дает 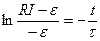или

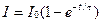, (3.22)

где 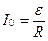представляет собой установившийся ток (при 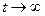). Из уравнения (3.22) видно, что быстрота установления тока определяется той же постоянной 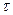. График зависимости 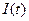– возрастания силы тока со временем показан на рис. 3.6 (кривая 2).

§ 5. Взаимная индукция

Взаимная индуктивность. Рассмотрим два неподвижных контура 1 и 2 (рис. 3.7), расположенные достаточно близко друг к другу.

Рис. 3.7.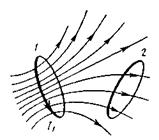

Если в контуре 1 течет ток 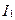, он создает через контур 2 полный магнитный поток Ф₂, пропорциональный (при отсутствии ферромагнетиков) току :

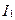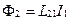(3.23)

Совершенно так же, если в контуре 2 течет ток 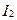, он создает через контур 1 полный магнитный поток

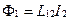(3.24)

Коэффициенты пропорциональност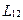и и 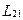называют взаимной индуктивностью контуров. Очевидно, взаимная индуктивность численно равна магнитному потоку сквозь один из контуров, создаваемому единичным током в другом контуре.

Коэффициенты 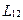и 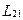зависят от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости окружающей контуры среды. Выражаются эти коэффициенты в тех же единицах, что и индуктивность L.

Теорема взаимности. Соответствующий расчет дает (и опыт его подтверждает), что при отсутствии ферромагнетиков коэффициенты L _|2 и L ₂₁ одинаковы:

L₁₂ = L₂₁. (3.25)

Это замечательное свойство взаимной индуктивности принято называть теоремой взаимности. Благодаря этой теореме можно не делать различия между 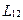и 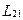, и просто говорить о взаимной индуктивности двух контуров.

Смысл равенства (3.25) в том, что в любом случае магнитный поток 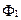, сквозь контур 1, созданный током 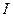в контуре 2, равен магнитному потоку Ф₂ сквозь контур 2, созданному таким же током 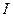в контуре 1. Это обстоятельство нередко позволяет сильно упрощать решение вопроса нахождении, например, магнитных потоков.

Однако наличие ферромагнетиков меняет дело, и теорема взаимности перестает выполняться.

Взаимная индукция – это явление возникновения ЭДС индукции в одном контуре при изменении тока в другом контуре. Наличие магнитной связи между контурами проявляется в том, что при всяком изменении тока в одном из контуров в другом контуре возникает ЭДС индукции. Это явление и называют в з а и м н о и индукцией.

Согласно закону электромагнитной индукции ЭДС, возникающие в контурах 1 и 2, равны соответственно:

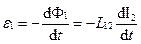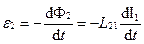, (3.26)

Здесь предполагается, что контуры неподвижны и ферромагнетиков поблизости нет.

На явлении взаимной индукции основан принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока.

Пример. В заключение этого параграфа оценим взаимную индуктивность двух коаксиальных неферромагнитных соленоидов [6] – соленоидов с общей осью. Пусть площади их поперечного сечения совпадают (S₁ =S₂=S), совпадают также их длины (l₁=l₂= l), а разными будут числа витков на единицу длины n₁ и n₂. Для расчета 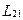пропустим ток 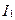по первому соленоиду и воспользуемся формулой (3.23):

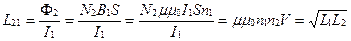(3.27)

где 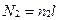- число витков

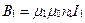
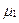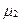и - соответственно магнитная проницаемость при токе 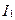и 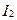, в отсутствие ферромагнетиков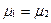

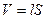
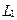и - и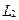ндуктивности коаксиальных соленоидов.

§ 6. Энергия магнитного поля

Пусть в цепи действует установившийся ток, который создает в окружающем пространстве магнитное поле. При отключении источника 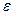ток, а вместе с ним и магнитное поле начнут исчезать. Элементарная работа тока за время исчезновенияd t равна

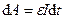, (3.28)

где 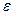и 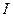– ЭДС самоиндукции и сила тока в произвольный момент времени t.

Если L = const, то .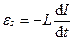

Следовательно,

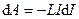. (3.29)

Проинтегрировав это выражение по 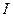(от 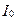до 0), мы получим полную работу, совершенную током за время, в течение которого исчезает магнитное поле:

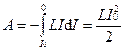. (3.30)

За счет работы (3.30) происходит увеличение внутренней энергии проводников, из которых образована цепь. Из законов термодинамики и опытов с электромагнитными волнами следует, что носителем энергии, за счет которой совершается работа (3.30), является магнитное поле. Таким образом, энергия магнитного поля W, созданного током 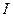, текущим в цепи с индуктивностью L, (в отсутствии ферромагнетиков) равна

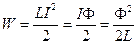. (3.31)

Энергию (3.31) можно выразить через характеристики магнитного поля.

Пусть цепь содержит длинный соленоид с сердечником из однородного магнетика. Индуктивность цепи примем равной индуктивности соленоида (индуктивность всех других элементов цепи мала по сравнению с индуктивностью соленоида). Индуктивность длинного соленоида равна

.

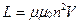Магнитное поле соленоида сосредоточено внутри соленоида. Индукция этого поля равна

,

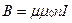откуда

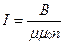
Подставив выражения для L и I в (3.31), получим

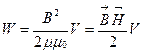. (3.32)

Магнитная энергия локализована в пространстве, занимаемом магнитным полем.

Магнитное поле длинного соленоида однородно. Следовательно, плотность энергии этого поля w (энергия единицы объема) равна

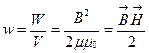. (3.33)

Формула (3.33) справедлива для любого поля — и однородного, и неоднородного. Если известна зависимость W от координат, то для нахождения энергии магнитного поля, распределенного в объеме V, нужно вычислить интеграл

. (3.34)

Замечание: Отметим, что выражения (3.32)–(3.34) относятся только к пара- и диамагнетикам. К ферромагнетикам они не применимы.

Отметим также, что магнитная энергия – величина существенно положительная. Это легко усмотреть из последних двух формул.

§ 7. Второе уравнение Максвелла. Ток смещения

Основная идея теории Максвелла заключалась во взаимосвязи между собой электрических и магнитных полей: если переменное магнитное поле порождает в окружающем пространстве электрическое поле (первое положение теории Максвелла), то в свою очередь и переменное электрическое поле должно создавать в окружающем пространстве магнитное поле. В связи с этим второе фундаментальное положение теории Максвелла гласит: переменное электрическое поле создает в окружающем пространстве магнитное поле.

Следовательно, в теореме о циркуляции вектора В (формула (1.15))

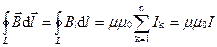
к источникам магнитного поля в виде токов проводимости добавляется ещё один источник, который Максвелл назвал током смещения. Током смещения Максвелл назвал количественную скалярную характеристику переменного электрического поля. (С современной точки зрения, термин не относится к числу удачных).

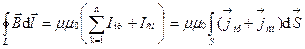(3.35)

Формула (3.35) получила название закона полного тока. В выражение (3.35) введены плотности тока проводимости (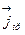) и смещения (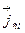), интеграл берётся по поверхности S, опирающейся на контур (L).

Плотность тока смещения 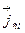связанас напряжённостью 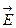и индукцией 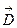переменного электрического поля:

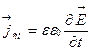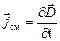, . (3.36)

В формуле (3.36) берётся частная производная от вектора Е и D по времени t.

Плотность полного тока .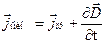

Ток проводимости (направленное движение заряженных частиц) и ток смещения (связан с переменным электрическим полем) имеют разную физическую природу, но они сходны по их способности создавать магнитное поле. Например, магнитное поле внутри конденсатора можно рассматривать как магнитное поле тока проводимости, текущего по проводнику конечных размеров с плотностью тока 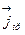, равной плотности тока смещения 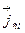. Это позволяет применять формулы магнитостатики для расчёта магнитного поля тока смещения. При этом линии вектора В тока смещения будут такими же, как и для тока проводимости.

Дата добавления: 2014-01-20