
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Полная система уравнений Максвелла в интегральной форме
|
|
|
|
 (1)
(1)
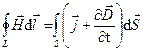 (2)
(2)
 (3)
(3)
 (4)
(4)
Величины, входящие в уравнения Максвелла, не являются независимыми и связаны так:
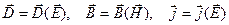 . (5, 6, 7)
. (5, 6, 7)
Для однородных изотропных неферромагнитных и несегнетоэлектрических сред формулы связи, выражаемые пятым, шестым и седьмым уравнениями, являются достаточно простыми:
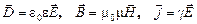 (5’, 6’, 7’)
(5’, 6’, 7’)
Третье и четвёртое уравнения Максвелла представляют собой теоремы Гаусса для электростатического и магнитного полей. Физический смысл этих уравнений состоит в следующем: источником электростатического поля являются свободные и связанные заряды; в природе отсутствуют магнитные заряды, т.е. линии вектора В магнитного поля являются замкнутыми.
Пятое и шестое уравнения Максвелла вводят векторы электрической индукции (электрического смещения) D и напряжённости Н магнитного поля, которые в отличие от истинных векторов E и B являются вспомогательными, вводимыми для удобства описания полей в присутствии вещества.
Седьмое уравнение Максвелла представляет собой закон Ома в дифференциальной форме, где g - удельная проводимость вещества.
Наиболее удобной является полная система уравнений Максвелла в дифференциальной форме

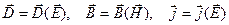
Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных. Источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.
Полная система уравнений Максвелла играет в электромагнетизме такую же роль, как законы Ньютона в механике.
§ 9. Электромагнитные волны
Этот парагграф перенести в раздел Колебания и волны
Следствием теории Максвелла является существование электромагнитного поля в виде электромагнитных волн (ЭМВ). ЭМВ – процесс распространения электромагнитного поля в пространстве. В основе образования ЭМВ лежат взаимные превращения электрического и магнитного полей: переменное магнитное поле порождает в окружающем пространстве переменное электрическое ноле, и это изменяющееся электрическое поле также создаёт в окружающем пространстве переменное магнитное поле и т.д. Процесс образования переменных электрического и магнитного полей охватывает всё новые и новые области пространства - в пространстве распространяется ЭМВ (рис. 3.8, здесь источником ЭМВ является текущий по проводнику переменный электрический ток ).
Рис. 3.8 
Решающую роль в утверждении максвелловской теории сыграли опыты Герца, согласно которым электрические и магнитные поля действительно распространяются в виде волн, поведение которых полностью описывается уравнениями Максвелла.
Волновое уравнение для векторов 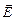 и
и 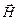 . Следствие уравнений Максвелла: векторы напряженностей
. Следствие уравнений Максвелла: векторы напряженностей 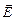 и
и 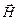 переменного электромагнитного поля для однородной и изотропной среды вдали от зарядов и токов удовлетворяют волновым уравнениям:
переменного электромагнитного поля для однородной и изотропной среды вдали от зарядов и токов удовлетворяют волновым уравнениям:
 , (9.1)
, (9.1)
где  (9.2)
(9.2)
оператор Лапласа, u— фазовая скорость.
Всякая функция, удовлетворяющая этим уравнениям, описывает некоторую волну. Следовательно, электромагнитные полямогут действительно существовать в виде электромагнитных волн.
Свойства электромагнитных волн:
Из уравнений Максвелла следует, что электромагнитные волны поперечны: векторы Е и В перпендикулярны к направлению распространения волны.
Закон изменения векторов Е и В в электромагнитной волне задается характером электромагнитных колебаний в излучающей антенне.
Электромагнитная волна называется плоской, если ее фазовая поверхность—плоскость.
Фазовая поверхность — поверхность, во всех точках которой векторы Е (или В) колеблются в одинаковых фазах.
Если модуль и направления вектора Е (равно как и вектора В) во всех точках фазовой поверхности одинаковы, то волна называется однородной.
Если векторы Е и В в плоской волне изменяются по гармоническому закону, волна называется гармонической.
Фазовая скорость электромагнитных волн – скорость перемещения данной фазовой поверхности, зависит от диэлектрической и магнитной проницаемости среды:  , где
, где  скорость света в вакууме.
скорость света в вакууме.
Мы видим, что в вакууме фазовая скорость электромагнитных волн совпадает со скоростью света.
Векторы 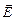 и
и 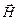 напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору
напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору  скорости распространения волны, причем векторы
скорости распространения волны, причем векторы 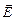 ,
, 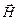 и
и  образуют правовинтовую систему.
образуют правовинтовую систему.
Из уравнений Максвелла следует также, что в электромагнитной волне векторы 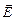 и
и 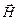 всегда колеблются в одинаковых фазах, причем мгновенные значения Е и Н в любой точке связаны соотношением
всегда колеблются в одинаковых фазах, причем мгновенные значения Е и Н в любой точке связаны соотношением
 .
.
Следовательно, Е и Н одновременно достигают максимума, одновременно обращаются в нуль и т. д.
Пусть плоская однородная гармоническая электромагнитная волна распространяется вдоль положительного направления оси х. Уравнения этой волны в векторном виде записываются следующим образом:
E = E mcosw(t – x/u), (9.3)
B = B mcosw(t – x/u), (9.4)
гдe E m=Еm j, B m=Bm k, (Em, Bm) — амплитуды векторов Е, В;
j, k — орты осей у, z;
w – угловая частота колебаний Е и В; х — координата точки наблюдения; u – фазовая скорость волны. Уравнениям (91.3) — (91.4) обычно придают следующий вид:
E=Emcos{wt – kx), (9.5)
B = Вmcos(wt – kx), (9.6)
где k =w/u=2p/l - волновое число.
На рис.3.9 изображена «мгновенная фотография» плоской гармонической электромагнитной волны.
рис.3.9 
Как видно из рисунка и из уравнений (9.5), (9.6), колебания векторов Е и В происходят в фазе: Е и В одновременно достигают максимума и одновременно проходят через нуль.
Гармоническая электромагнитная волна характеризуется частотой, периодом и длиной.
Период Т — время, в течение которого вектор Е (или В) в электромагнитной волне совершает одно полное колебание.
Частота n — число полных колебаний за единицу времени.
Длина волны l— расстояние, на которое волна распространяется за один период:
 (9.7)
(9.7)
Электромагнитная волна материальна. Она обладает массой, энергией, импульсом.
Энергия электромагнитной волны складывается из энергии электрического и магнитного полей. Объемная плотность w энергии электромагнитной волны  .
.
Для характеристики переноса энергии электромагнитной волной вводят понятие потока энергии.
Поток энергии Ф w через поверхность S — энергия, протекающая через S за единицу времени.
Распределение потока энергии по поверхности характеризует плотность потока энергии— векторная физическая величина, численно равная энергии, переносимой за единицу времени через единичную площадку, перпендикулярную к направлению распространения волны, и совпадающая с направлением фазовой скорости волны. Вектор плотности потока энергии называется вектором Умова-Пойнтинга 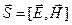 . Направление вектора
. Направление вектора  совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН.
совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН.
Масса электромагнитной волны, заключенная в некотором объеме V, может быть вычислена по формуле теории относительности о соотношении массы и энергии:
W=mc2 (9.16)
В частности, масса, заключенная в единице объема (средняя плотность материи в электромагнитной волне) r, равна
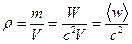 (9.17)
(9.17)
где  – средняя плотность энергии волны.
– средняя плотность энергии волны.
Импульс некоторого объема электромагнитной волны
k =m c (в вакууме),
k =m u (в среде).
Электромагнитная волна, встречая на своем пути тела, оказывает на них давление. Пусть плоская волна падает на плоскую поверхность тела перпендикулярно к поверхности (рис. 3.10).
 рис.3.10
рис.3.10
Электрическое поле волны вызовет в этом теле ток (проводимости или поляризации). Магнитное поле волны будет действовать на этот ток с силой, направление которой совпадает с направлением распространения волны. Пусть рассматриваемое тело полностью поглощает падающую на него волну. Тогда импульс, передаваемый волной поверхности тела S за время D t, равен тс, где т — масса волны, заключенная в прямой призме с основанием S и высотой c D t (см. рис. 3.10). Импульс тс равен <f>Dt, где < f > — средняя сила, действующая на площадку S:
mc=<f> D t. (9.18)
Энергия электромагнитной волны, заключенная в объеме Sc D t, равна, с одной стороны,
W=mc2 (9.19)
с другой,
W=<w>Sc D t, (9.20)
где <w> — средняя плотность энергии волны.
Из (9.19) и (9.20) находим т и подставляем в (9.18):
< w >S= <f>
Разделив <f> на S, найдем давление:
 (9.21)
(9.21)
Если тело частично отражает волну и k — коэффициент отражения, то давление равно
p =(1+ k)< w > (9.22)
(коэффициент отражения показывает, какая доля падающей на тело энергии отражается).
Для абсолютно отражающего тела k= 1и
p =2< w >. (9.23)
Если волна падает на поверхность под углом i к нормали, то
p =(1+ k)< w >cos i. (9.24)
При прохождении через границу раздела двух сред электромагнитная волна испытывает преломление. Электромагнитные волны могут интерферировать, дифрагировать. Электромагнитные волны могут быть поляризованными (обо всем этом пойдет речь в следующей части курса).
Теория Максвелла сыграла выдающуюся роль в развитии физики. Эта теория не только объяснила большую совокупность опытных фактов, но и предсказала вплоть до количественных оценок существование неизвестных ранее явлений, таких как давление электромагнитных волн, электромагнитная природа света и др.
Основная литература
1. Савельев И.В. Курс общей физики Т.2 М.,1982
2. Сивухин Д.В. Электричество. - М.: Высшая школа, 1985, 688 с.
3. Калашников С.Г. Электричество. Учебное пособие. - М.: Наука, 1985, 592 с.
Дополнительная литература
1. Матвеев А.Н. Электричество и магнетизм. Учебное пособие. - М.: Высшая школа, 1989, 463 с.
2.Иродов И.Е. Основные законы электромагнетизма: Учебное пособие. - М.: Высшая школа, 1991, 203 с.
3. Электричество и магнетизм. Берклеевский курс физики. - М.: Иностранная литература, 1984.
этих скоростей в формуле (159.1) надо брать их проекции на направление этой прямой.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1028; Нарушение авторских прав?; Мы поможем в написании вашей работы!