Магнитное поле прямого тока

Ток течет по прямому проводу бесконечной длины. В качестве постоянной интегрирования выберем угол α.

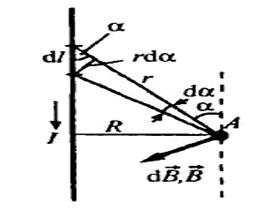
Из рисунка ,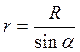

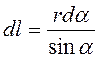
Следовательно dB =

Угол α для всех элементов прямого провода изменяется от 0 до 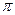. По принципу суперпозиции:

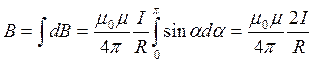
если ток течет по отрезку провода (см. рисунок), то:

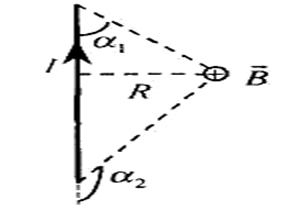
Эта формула переходит в формулу для бесконечного длинного проводника при α ₁ = 0, α ₂ =π.

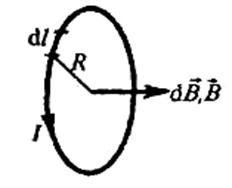
9. Магнитное поле в центре кругового тока.

В данном случае сложение векторов можно заменить сложением их модулей, учитывая 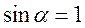, r=R:

откуда

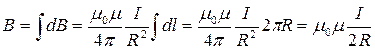
Можно показать, что на расстоянии r от центра витка вдоль оси витка магнитное поле будет:

Напряженность магнитного поля, создаваемого круговым током на большом расстоянии от витка с током (r>> R):

где р_т = IS - магнитный момент витка с током.

Сравним эту формулу с формулой для электрического поля диполя (с электрическим дипольным моментом р_е) на оси диполя (см. З-п.13):

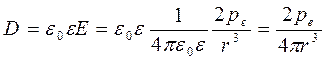
Очевидное подобие этих формул объясняет, почему часто говорят, что контур с током подобен "магнитному диполю", имеющему равный с контуром магнитный момент.

10. Закон Ампера.

Действие магнитного поля на рамку с током - это пример воздействия магнитного поля на проводник с током. Ампер установил, что сила d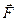, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, равна:

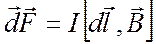
где d- вектор по модулю равный dl и совпадающий по направлению с током, 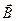- вектор магнитной индукции.

Наглядно направление силы Ампера принято определять по правилу левой руки, если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера.

11. Взаимодействие параллельных токов.

Закон Ампера применяется для определения силы взаимодействия двух токов.

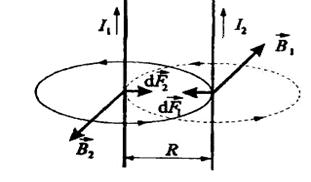
Два параллельных проводника с токами I₁, и I₂ находятся на расстоянии

R друг от друга. Направление сил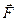 d₁ и d, с которыми поля ₁ и 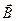₂ действуют на проводники с токами I₂ и I₁, определяются по правилу левой руки.

,

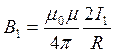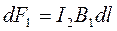
Отсюда: 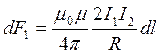. Аналогично

, ,

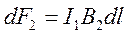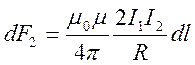. Таким образом:

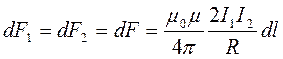
Проводники с токами одинакового направления притягиваются, с токами разного направления - отталкиваются.

12. Магнитная постоянная.

В системе СИ единица измерения силы тока - ампер - вместе с килограммом, метром и секундой является основной единицей. По определению "ампер есть сила неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 метра один от другого в вакууме, вызвал бы между этими проводниками силу, равную 2∙ 10 ^-7 ньютона на каждый метр длины".

В вакууме (μ =1) сила взаимодействия на единицу длины проводника

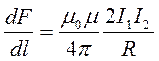
при I₁ =I₂ =1А и R=1м: 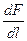=2∙10 ^-7 Н/м. Отсюда

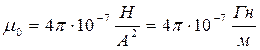
где генри (Гн) - единица индуктивности - будет определена позднее.

13. Единицы магнитной индукции и напряженности магнитного поля.

Пусть элемент проводника dl с током I перпендикулярен направлению магнитного поля. Закон Ампера dF = IBdl, откуда

Единица магнитной индукции В - тесла (Тл) - магнитная индукция такого однородного магнитного поля, которое действует с силой 1Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно

направлению поля, если по этому проводнику проходит ток 1А:

1 Тл =1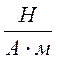

Из формулы В =μ_оμН в вакууме (μ = 1) получим Н = .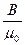

Единица напряженности магнитного поля Н - ампер на метр (А/м) -

напряженность такого поля, индукция которого в вакууме равна 4π·10 ^-7 Тл

14. Магнитное поле свободно движущегося заряда.

Проводник с током создает вокруг себя магнитное поле. Электрический ток - это упорядоченное движение электрических зарядов. Магнитное поле 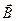точечного заряда q, свободно движущегося с постоянной нерелятивистской

скоростью 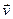(v «с):

,

где r - радиус-вектор, проведенный из заряда q к точке наблюдения, α- угол между 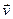и .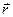

15. Сила Лоренца.

Так же как и на проводник с током, магнитное поле действует и на отдельный заряд, движущийся в магнитном поле.

Сила, действующая на электрический заряд q, движущийся в магнитном

поле 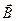со скоростью и, называется силой Лоренца:

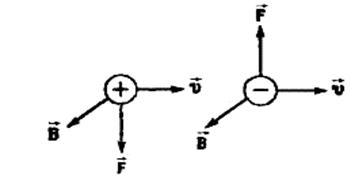
F = q[v,B]

или F = qvBsinα, где α - угол между и .

Направление силы Лоренца, так же как и силы Ампера, определяется по правилу левой руки. Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы. Поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает.

Постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.

Движение заряда, на который кроме магнитного поля с индукцией действует и электрическое поле с напряженностью 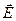описывается формулой Лоренца:

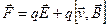
16. Движение заряженных частиц в магнитном поле.

Считаем, что магнитное поле однородно и на частицы не действуют электрические поля. Рассмотрим три возможных случая:

1. 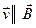Заряженная частица движется в магнитном поле вдоль линий магнитной индукции (угол α между векторам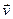и и 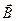равен 0 или π ). Сила Лоренца равна нулю. Магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

2. 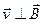- Заряженная частица движется в магнитном поле перпендикулярно линиям магнитной индукции (угол α = π12).

Сила Лоренца F = qvB: постоянна по модулю и нормальна к траектории частицы. Частица будет двигаться по окружности радиуса R с центростремительным ускорением а_n =. Из второго закона Ньютона

qvB =

получаем радиус окружности R =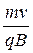 и период вращения .

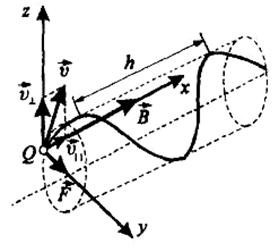
3. Заряженная частица движется под углом αк линиям магнитной индукции. Движение частицы можно представить в виде суммы двух движений:

1) равномерного прямолинейного движения вдоль поля со скоростью

v _║ =vcos α,

2) равномерного движения по окружности в плоскости, перпендикулярной полю.

Суммарное движение будет движением по спирали, ось которой параллельна магнитному полю. Шаг винтовой линии h = v_║ T = vTcosα, где

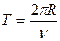-период вращения частицы, и R =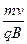

Если магнитное поле неоднородно и заряженная частица движется под углом к линиям магнитного поля в направлении возрастания поля, то величины R и hуменьшаются с ростом 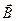. На этом основана фокусировка заряженных частиц магнитным полем.

17. Эффект Холла.

Эффект Холла - это возникновение электрического поля в проводнике или полупроводнике с током при помещении его в магнитное поле.

Эффект Холла - следствие влияния силы Лоренца на движение носителей тока. В магнитном поле 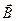при протекании через проводник тока с плотностью устанавливается электрическое поле с напряженностью

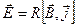где R - постоянная Холла.

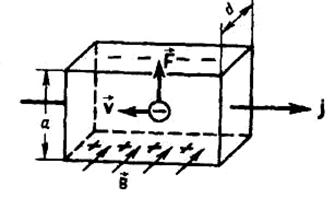
Пусть, например, металлическая пластинка с током расположена в магнитном поле перпендикулярном току (см. рисунок). Сила Лоренца приводит к повышению концентрации носителей тока - электронов - у верхнего края пластинки. При этом верхний край зарядится отрицательно, а нижний, соответственно - положительно. Стационарное распределение зарядов будет достигнуто, когда действие созданного таким образом электрического поля

уравновесит силу Лоренца:

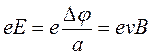или 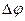= vBa, где а- ширина пластинки, е - заряд электрона, 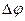- поперечная (холловская) разность потенциалов.

Поскольку сила тока I=jS = nevS (S=ad - площадь поперечного сечения пластинки толщиной d и шириной а, n - концентрация электронов,

v- средняя скорость упорядоченного движения электронов), то

Знак постоянной Холла R = совпадает со знаком носителей тока,

поэтому эффект Холла используют для определения природы носителей тока в веществах и определения их концентрации.

18. Теорема о циркуляции вектора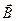

Циркуляцией вектора 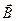по заданному замкнутому контуру L называется следующий интеграл по этому контуру: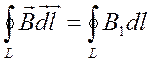

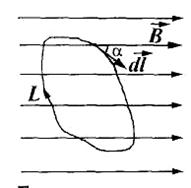
где dl - элемент длины контура, направленный вдоль обхода контура; B _l =Bcosα – составляющая вектора 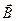в направлении касательной к контуру, с учетом выбранного направления обхода; α - угол между векторами и .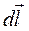

Теорема о циркуляции вектора 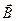(закон полного магнитного поля в вакууме): циркуляция вектора 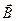по произвольному замкнутому контуру равна произведению магнитной постоянной μ ₀ на алгебраическую сумму токов, охватываемых этим контуром:

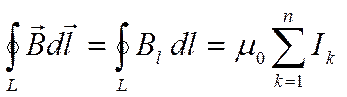
где п- число проводников с токами, охватываемых контуром L произвольной формы.

Эта теорема справедлива только для поля в вакууме, поскольку для поля в веществе надо учитывать молекулярные токи.

Каждый ток учитывается

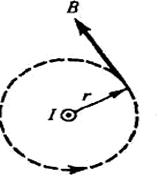
столько раз, сколько он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта.

Пример: магнитное поле прямого тока. Замкнутый контур представим в виде окружности радиуса r. В каждой точке этой окружности вектор 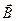одинаков по модулю и направлен по касательной к окружности:

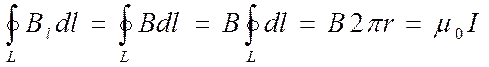, отсюда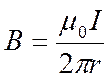

Сравним выражения для циркуляции векторов 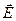и .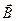

,

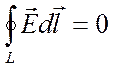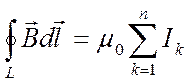
Принципиальное различие между этими формулами в том, что циркуляция вектора Е электростатического поля всегда равна нулю. Такое поле является

Дата добавления: 2014-01-20