
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обработки данных косвенных измерений методом переноса погрешностей
|
|
|
|
Косвенные измерения
Измерения называются косвенными, если их результат вычисляется по формулам, в которые подставляются результаты прямых измерений. Пусть нам необходимо определить функции f = f (x, y, z) от непосредственно измеренных величин x, y, z. Функция f предполагается дифференцируемой по всем переменным; кроме того, предполагается, что на интервалах, куда попадают значения x, y, z, функция f не имеет нулей частных производных. Обозначим fi = f (xi, yi, zi).
Используется в случае, когда каждая из величин x, y, z, представляющих собой аргументы функции, измеряется независимо от остальных в своей серии опытов, и эти величины образуют выборки (близки друг к другу). Число опытов в сериях, вообще говоря, не обязано быть одинаковым, требуется только неизменность условий для прямо измеряемой величины в своей серии, неизменность условий для f во всех сериях и взаимная независимость всех опытов.
1. По формулам прямых измерений определить величины 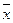 ,
, 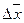 ;
;  ,
,  ;
;  ,
,  (с учётом приборных погрешностей).
(с учётом приборных погрешностей).
2. Рассчитать значение функции 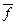 = f (
= f (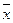 ,
, ,
,  ).
).
3. Вычислить частные производные от функции 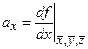 ,
, 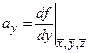 ,
,  или, для легко логарифмируемой функции f, от ее логарифма
или, для легко логарифмируемой функции f, от ее логарифма  в точке
в точке 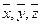 .
.
4. Вычислить полную погрешность функции  (формула переноса погрешностей) или по эквивалентной формуле для легко логарифмируемой функции:
(формула переноса погрешностей) или по эквивалентной формуле для легко логарифмируемой функции:  .
.
5. Записать результат измерения и округлить его.
6. Свести результаты обработки эксперимента в таблицу 2.
| Таблица 2. | |||||||||
| xi | q x= | ||||||||
| yi | q y= | ||||||||
| x↑i | 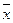 =, Rx=x↑ N –x↑ 1 = =, Rx=x↑ N –x↑ 1 =
| ||||||||
| xi+ 1 -xi | UP,N Rx = | ||||||||
D xi = xi – 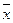
| SD xi = 0 | ||||||||
| (D xi)2 | S(D xi)2 = | ||||||||
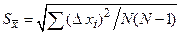 =, =,  , ,
 , , 
| |||||||||
| y↑i |  =, Ry=y↑N –y↑ 1 = =, Ry=y↑N –y↑ 1 =
| ||||||||
| yi+ 1 -yi | UP,N Ry = | ||||||||
D yi = yi – 
| SD yi = 0 | ||||||||
| (D yi) 2 | S(D yi)2 = | ||||||||
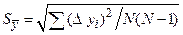 =, =, 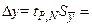 , ,
 , , 
| |||||||||
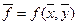 =, =,  = =
| |||||||||
 
| |||||||||
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 2519; Нарушение авторских прав?; Мы поможем в написании вашей работы!