Где а - положительное число

Наша з а д а ч а - найти функцию u (x,t), график которой дает форму струны в любой момент времени t, т. е. найти решение уравнения (1) при граничных:

(2)

и начальных условиях:

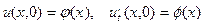(3)

Сначала будем искать решения уравнения (1), удовлетворяющие граничным условиям(2). Нетрудно увидеть, что u (x, t)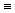0 является решением уравнения (1), удовлетворяющие граничным условиям(2). Будем искать решения, не равные тождественно 0, представимые в виде произведения u (x,t)= X (x) T (t), (4), где , .

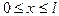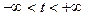Подстановка выражения (4) в уравнение (1) дает:

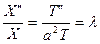
Из которого наша задача сводится к отысканию решений уравнений:

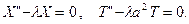
Используя это условие X (0)=0, X (l)=0, докажем, что 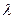отрицательное число, разобрав все случаи.

a) Пусть 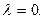Тогда X ”=0 и его общее решение запишется так:

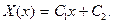
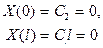
откуда 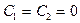и 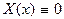,что невозможно, так как мы рассматриваем решения, не обращающиеся тождественно в нуль.

б) Пусть 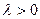. Тогда решив уравнение

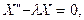
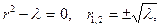
получим 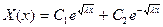, и, подчинив, найдем, что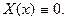

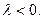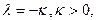в) Если то

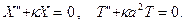
Уравнения имеют корни:

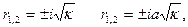
получим:

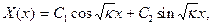
где 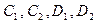-произвольные постоянные. Из начального условия найдем:

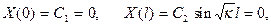
откуда 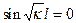, т. е.

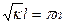(n =1,2,...)

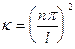(n =1,2,...).

Учитывая это, можно записать:

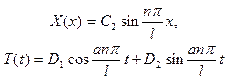(n=1,2,...).

и, следовательно

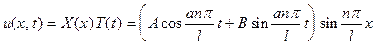, (n =1,2,...),

но так как A и B разные для различных значений n то имеем

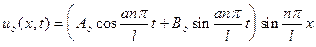, (n =1,2,...),

где 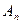и произвольные постоянные, которые попытаемся определить таким образом, чтобы ряд удовлетворял уравнению (1), граничным условиям (2) и начальным условиям (3).

Итак, подчиним функцию u (x,t) начальным условиям, т. е. подберем 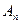и 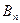так, чтобы выполнялись условия

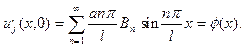
Эти равенства являются соответственно разложениями функци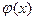й и 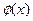на отрезки [0, l ] в ряд Фурье по синусам. (Это значит что коэффициенты будут вычисляться как для нечетной функций). Таким образом, решение о колебании струны с заданным граничными и начальными условиями дается формулой

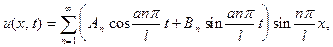
где

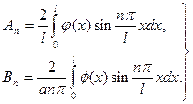(n =1,2,...)

Дата добавления: 2014-01-20