Разложение функций в тригонометрический ряд Фурье

Исходные данные:

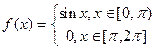(Рис. 1)

Функция периодическая с периодом 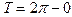.(f(x+T)=f(x)) Функция имеет на промежутке конечное число точек разрыва первого рода.

Сумма ряда в точках функции сходится к значению самой функции, а в точках разрыва к величин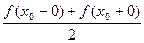е , где 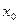-точки разрыва.

Рис. 1

Производная также непрерывна везде, кроме конечного числа точек разрыва первого рода. Вывод: функция удовлетворяет условию разложения в ряд Фурье.

1) F(x) - кусочно-непрерывна на интервале .

2) F(x) - кусочно-монотонна.

Так как отсутствует симметрия относительно OY, а также центральная симметрия - то рассматриваемая функция произвольна.

Представление функции рядом Фурье.

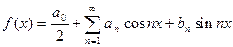
Из разложения видим, что при n нечетном принимает значения равные 0, и дополнительно надо рассмотреть случай когда n=1.

Поэтому формулу для можно записать в виде:

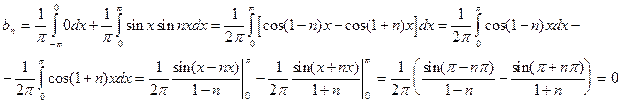
(так как ).

Отдельно рассмотрим случай когда n=1:

.

Подставим найденные коэффициенты в 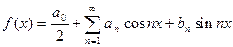получим:

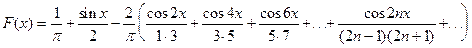
и вообще

.

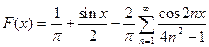Найдем первые пять гармоник для найденного ряда:

1-ая гармоника ,

2-ая гармоника ,

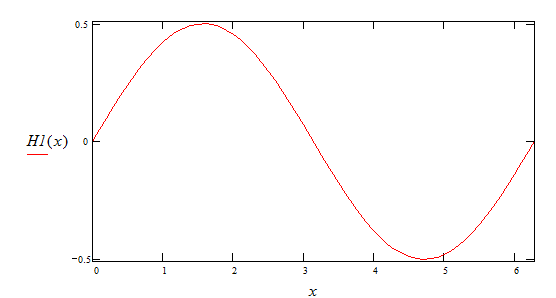
3-ая гармоника ,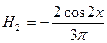

4-ая гармоника ,

5-ая гармоника ,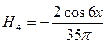

и общий график F(x), сумма выше перечисленных гармоник. и сами гармоники.

Запишем комплексную форму полученного ряда

Для рассматриваемого ряда получаем коэффициенты (см. теорию)

,

но при не существует, поэтому рассмотрим случай когда n =+1:

(т.к. см. разложение выше)

и случай когда n =-1:

(т.к. )

И вообще комплексная форма:

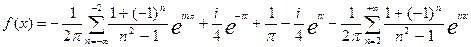
или

или

Разложение четной функции в ряд

Данную выше функцию сделаем четной(см. теорию), и рассмотрим ее на промежутке от 0 до смотри рис.2

Рис.2

поэтому разложение по косинусу имеет вид:

Из разложения видим что при n =2 дробь теряет смысл поэтому отдельно рассмотрим разложения первого и второго коэффициента суммы:

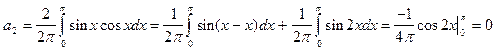
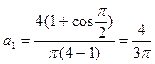
На основе данного разложения запишем функцию в виде ряда:

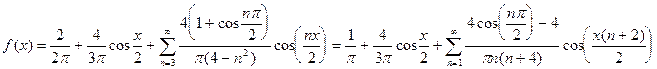
и вообще

.

Найдем первые пять гармоник для найденного ряда:

1-ая гармоника

2-ая гармоника

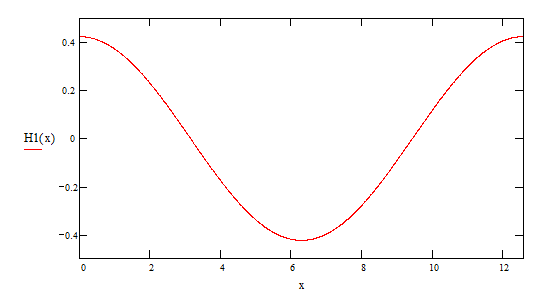
3-я гармоника

4-ая гармоника

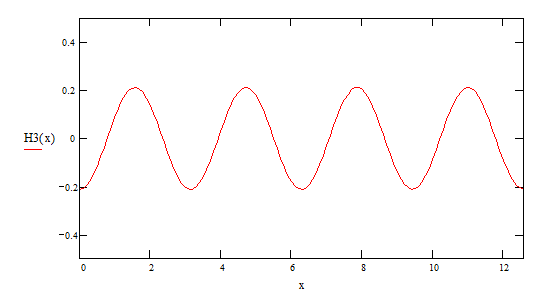
5-ая гармоника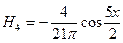

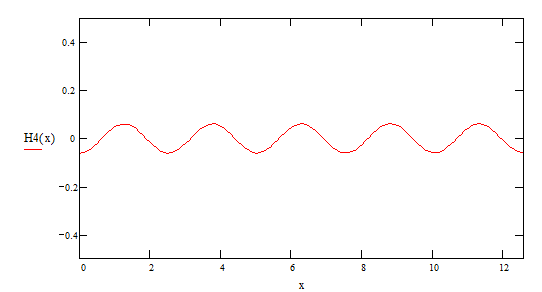
А теперь рассмотрим сумму этих гармоник F(x):

Комплексная форма ряда по косинусам

Для рассматриваемого ряда получаем коэффициенты (см. гл.1)

,

но при не существует, поэтому рассмотрим случай когда n =+2:

(т.к. см. разложение выше)

и случай когда n =-2:

(т.к. )

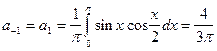
И вообще комплексная форма:

или

или

Разложение нечетной функции в ряд

Аналогичным образом поступаем с данной функцией F(x), продлевая ее как нечетную, и рассматриваем на промежутке от 0 до смотри рис.3

Рис.3

поэтому разложение по синусам имеет вид:

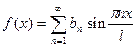
Из данного разложения видно, что при n =2 произведение неопределенно (можно не учесть часть суммы), поэтому рассмотрим два отдельных случая.

При n =1:

,

и при n =2:

Учитывая данные коэффициенты имеем разложения в виде

и вообще

Найдем первые пять гармоник для данного разложения:

1-ая гармоника

2-ая гармоника

3-ая гармоника

4-ая гармоника

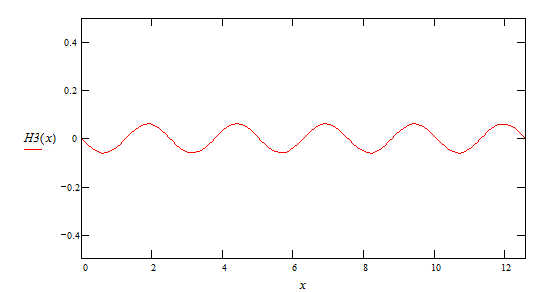
5-ая гармоника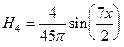

И просуммировав выше перечисленные гармоники получим график функции F (x)

Вывод:

На основании главы 2, разложение функции в тригонометрический ряд(рис.1), разложение в ряд по косинусам(рис.2), разложение по синусам(рис.3), можно заключить, что данная функция разложима в тригонометрический ряд и это разложение единственное. И проанализировав суммы первых пяти гармоник по каждому разложению можно сказать, что наиболее быстрее к заданному графику достигается при разложении по синусам.

Комплексная форма ряда по синусам

Основываясь на теорию (см. гл.1) для ряда получаем:

, (т.к. )

тогда комплексный ряд имеет вид:

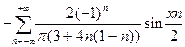
ГЛАВА 3

ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ

Проверка условий представимости

Данную ранее функцию (см. гл. 2) доопределим на всей прямой от до как равную нулю(рис.4).

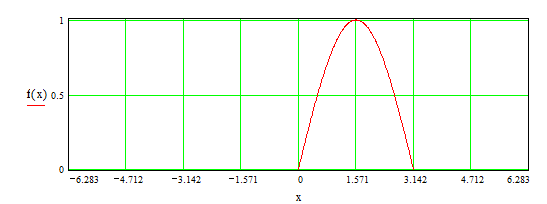
Рис.4

а) f(x)-определенна на R;

б) f(x) возрастает на , f(x) убывает на 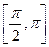- кусочнo-монотонна.

f(x) = const на и .

< .

И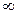нтеграл Фурье

В соответствии с теорией (см. гл. 1) найдем a (u) и b (u):

;

.

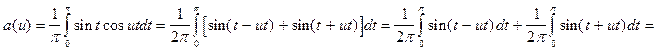
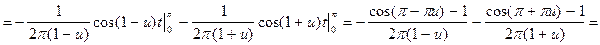
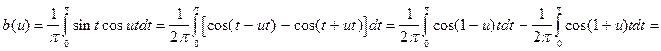
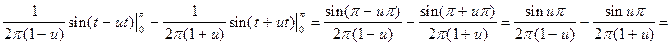
И в конечном варианте интеграл Фурье будет выглядеть так:

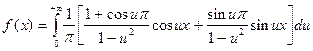
Интеграл Фурье в комплексной форме

Теперь представим интеграл Фурье в комплексной форме. На основе выше полученных разложений имеем:

,

,

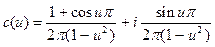а теперь получим интеграл в комплексной форме:

.

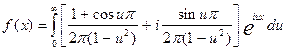ГЛАВА 4

ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ПОЛИНОМОМ ЛЕЖАНДРА

Основные сведения

Функцию можно разложить в ортонормированной системе пространства X=[-1,1], причем полиномы получим, если проинтегрируем выражение:

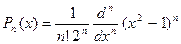
Соответственно получим для n=0,1,2,3,4,5,...:

..........

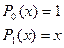
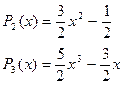
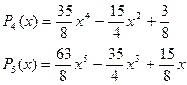
Для представления функции полиномом Лежандра необходимо разложить ее в ряд:

,

где и разлагаемая функция должна быть представлена на отрезке от -1 до 1.

Преобразование функции

Наша первоначальная функция имеет вид (см. рис. 1):

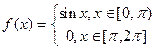
т. к. она расположена на промежутке от 0 до необходимо произвести замену, которая поместит функцию на промежуток от -1 до 1.

Замена:

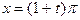
и тогда F(t) примет вид

или

Вычисление коэффициентов ряда

Исходя из выше изложенной формулы для коэффициентов находим:

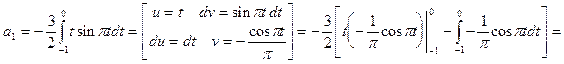
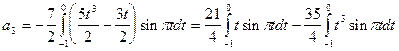
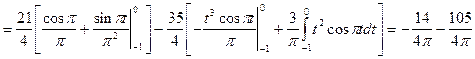
Далее вычисление коэффициентов осложнено, поэтому произведем вычисление на компьютере в системе MathCad и за одно проверим уже найденные:

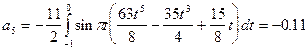
Рассмотрим процесс стремления суммы полинома прибавляя поочередно 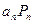- слагаемое:

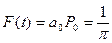
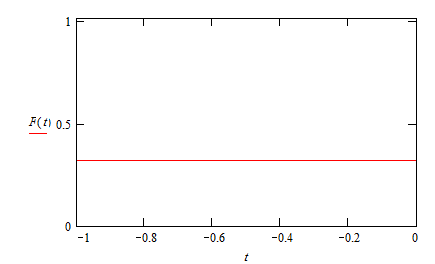
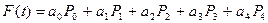
А теперь рассмотрим график суммы пяти полиномов F (t) на промежутки от -1 до 0 (рис.5):

Рис. 5

т.к. очевидно, что на промежутке от 0 до 1 будет нуль.

Вывод:

На основе расчетов гл.2 и гл.4 можно заключить, что наиболее быстрое стремление из данных разложений к заданной функции достигается при разложении функции в ряд.

ГЛАВА 5

ДИСКРЕТНЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ

Прямое преобразование

Для того, чтобы произвести прямое преобразование, необходимо задать данную функцию (гл. 1, рис. 1) таблично. Поэтому разбиваем отрезок от 0 до на N =8 частей, так чтобы приращение:

В нашем случае , и значения функции в k -ых точках будет:

для нашего случая (т.к. a =0).

Составим табличную функцию:

k
		0.785	1.571	2.356	3.142	3.927	4.712	5.498
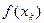
		0.707		0.707

Табл. 1

Прямым дискретным преобразованием Фурье вектора называется 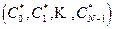. Поэтому найдем:

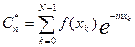, n =0,1,..., N -1

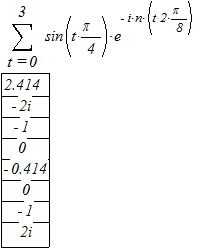
Сумму находим только до 3 слагаемого, т.к. очевидно, что от 4 до 7 к сумме суммируется 0 (т.к. значения функции из таблицы равны нулю).

Составим таблицу по прямому дискретному преобразованию:

зная, , где

, где

n
	2,4				0.4
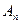
	0.318	0.25	0.106		0.021		0.009

Табл. 2

Амплитудный спектр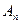

Обратное преобразование

Обратимся к теории гл.1. Обратное преобразование- есть функция:

В нашем случаи это:

А теперь найдем модули и составим таблицу по обратным дискретным преобразованиям:

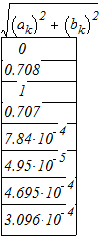
k
		0.785	1.571	2.356	3.142	3.927	4.712	5.498
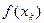
		0.707		0.707
		0.708		0.707	8e-4	5e-5	5e-4	3e-4

Табл. 3

Из приведенной таблицы видно, что 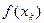приближенно равно .

Построим графики используя табл.3, где 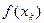- это F (k), а - это f (k) рис. 6:

Рис. 6

Вывод:

На основе проделанных расчетов можно заключить, что заданная функция представима в виде тригонометрического ряда Фурье, а также интеграла Фурье, полинома Лежандра и дискретных преобразований Фурье. О последнем можно сказать, что спектр (рис. 6) прямого и обратного преобразований совпадают с рассматриваемой функцией и расчеты проведены правильно.

Дата добавления: 2014-01-20