Формальные грамматики и языки

Государственное и межгосударственное регулирование движения капитала.

Все возрастающее воздействие международного движения капитала на национальную экономику приводит к сохранению государственного и международного регулирования движения капитала, несмотря на тенденцию к его либерализации. На национальном уровне регулируется преимущественно экспорт капитала, на международном уровне - главным образом движение прямых инвестиции.

Меры государственного регулирования экспорта и импорта капитала можно разделить на меры по ограничению движения капитала и меры по его поддержке - они должны быть взаимосвязаны.

Меры по ограничению вывоза капитала:

− необходимость получения предварительного разрешения;

− запрет или ограничение некоторых видов инвестиций за рубежом;

− ограничения на финансирование вывоза капитала;

− соблюдение ряда предварительных условий.

Меры по поддержке инвестирования за рубежом:

− информационная и техническая поддержка;

− прямая финансовая поддержка и налоговые льготы;

− страхование инвестиций.

Международное (двустороннее, региональное и многостороннее) регулирование движения капитала.

Двустороннее - соглашения о поощрении взаимной защиты инвестиций, об избежании двойного налогообложения.

Региональные - ЕС и НАФТА.

Можно формально определить язык как подмножество множества всех предложений из «слов» или символов некоторого основного словаря.

Например, язык Си состоит из программ, которые являются последовательностями, состоящими из {, }, if, for, while, ….

Алфавит – это непустое множество элементов. Назовём элементы алфавита символами (алфавит не обязан быть конечным или счётным, но во всех практических приложениях он будет конечным) (может счётным.

Всякая конечная последовательность символов алфавита А называется цепочкой.

Вот несколько цепочек в алфавите A = { a, b, c }: a, b, c, ab, aabb. Мы также допускаем существование пустой цепочки λ (е), т.е. цепочки не содержащей ни одного слова. Порядок символов в цепочке важен. Так цепочка аб, не то же самое что и ба. Длинна цепочки х - | x | - равна числу символов в цепочке.: | λ |=0, | a |=1, | abc |=3.

Будем использовать буквы a, b, c, как имена символов алфавита, в то время как x, y, z, w – для обозначения цепочек символов.

Если х и у - цепочки, то их конкатенация ху является цепочкой, полученная путём дописывания символов цепочки у вслед за символами цепочки х. Если х = dе и у = ес, то ху = dеес.

Т.к. пустая цепочка λ не содержит символов, то λх = х λ = х.

Если z = xy – цепочка, то х голова, а у – хвост z. И наконец, х – правильная голова, если у – непустая цепочка (не λ), у – правильный хвост, если х – не λ.

Если х = абс, то λ, а, аб, абс – голова, все правильные, кроме абс. (Будем обозначать множество цепочек заглавными буквами).

Произведение АB двух множеств цепочек А и B определяется как AB = { xy | x A, y B }. Пусть А ={ a, b } и B ={ c, d }, то AB ={ ac, ad, bc, bd }

Т.к. λх = х λ = х для любой цепочки, то { λ } A = A { λ }= A (множество из пустых цепочек можно и слева, и справа домножать).

Определим степень цепочки:

x ⁰ – пустая цепочка λ

x ¹ = х

x ²= хх

x ³= ххх

…

x ⁿ= xx ^n-1= x ^n-1x (n>0)

Аналогично определяется степень алфавита А:

А ⁰={ λ }, A ¹=1, …, A ⁿ= AA ^n-1= A ^n-1 A, n>0

Определим 2 операции:

Итерацию А * множества А: А *= А ⁰A⁺ и усечённую итерацию А ⁺ множества А: А ⁺= А ¹ A ²… A ⁿ…

Таким образом, если A ={ a, b }, то А * включает цепочки λ, а, б, аа, аб, ба, ааа, ааб, бб, ….

А ⁺= АА *= А * А

Определение 1:

Продукцией или правилами подстановки называется упорядоченная пара(u, х), которая записывается так u::=х, где u – символ, а х – непустая конечная цепочка символов, где u – называется левой частью правила, х – правой.

Определение 2:

Грамматикой G [ z ] называется конечное, непустые множество правил.

z – это символ, который должен встретиться в левой части по крайней мере одного правила.

Он называется начальным символом. Все символы, которые встречаются в левых и правых частях правил, образуют словарь V.

Пример:

Грамматика G1 [<число>]

<число>::=<пчс>

<пчс>::=<пчс><цифра>

<пчс>::=<цифра>

<цифра>::=0

<цифра>::=1

…

<цифра>::=9

Словарь V для этой грамматики следующий:

V ={0,1,2,3,4,5,6,7,8,9, <цифра>,<пчс>,<число>}.

Определение 3:

В заданной грамматике G символы, которые встречаются в левой части правил, называются нетерминальными. Они образуют множество нетерминальных символов V_N. Символы, которые не входят в множество V_N, называется терминальными. Они образуют множество V_T. Таким образом V = V_N V_T.

Нетерминалы будем заключать в угловые скобки < >, чтобы отличить их от терминалов.

В грамматике G1 символы 0,1,2,3,…,9 – терминалы; число, ПЧС, цифра - нетерминалы.

Множество правил с одинаковой левой частью будем записывать V::x|y|…|z.

Тогда G1 будет выглядеть следующим образом:

<число>::=<пчс>

<пчс>::=<пчс><цифра>/<цифра>

<цифра>::=0|1|2|3|…|9

Такая форма записи называется нормальной формой Бэкуса (НФБ) или формой Бэкуса – Наура.

Определение 4:

Пусть G – грамматика. Мы говорим, что цепочка V непосредственно порождает цепочку wu и обозначаем V => w, если для некоторых цепочек х и у можно написать: V = xUy, w = хuу где U::= u – правило грамматики G. Мы также говорим, что w - непосредственно выводима из V, цепочки х и у могут быть пустыми.

Пример:

V	w	Использованные пр.	x	y
<число>=> <пчс>=> <пчс><цифра>=> <цифра><цифра>=> 7<цифра>=>	<пчс> <пчс><цифра> <цифра><цифра> 7<цифра>		λ λ λ λ	λ λ <цифра> <цифра> λ

Определение 5:

Говорят V порождает w V =>⁺ w, если существует последовательность непосредственных выводов V = u ₀=>u₁=>u₂=>…=>u_n= w n>0. Эта последовательность называется выводом длины n.

Говорят, также, что цепочка u является выводом V. Наконец пишут V =>* w, если V =>+ w или V= w;

Пример:

<число>=><пчс>=><пчс><цифра>=><цифра><цифра>=>7<цифра>=>75, таким образом <число>=>75 и длинна вывода = 5.

Если в цепочке есть хотя бы 1 нетерминал, из неё можно вывести новую цепочку. Однако, если нетерминальные символы отсутствуют, то вывод надо закончить.

Каким будет язык, отписанный грамматикой G1[<число> ]?

Следующим определением утверждается, что этим конкретным языком является множество последовательностей из одной и более цифр.

Определение 6:

Пусть G [ z ] – грамматика. Цепочка х называется сентенциальной формой, если х выводима из начального символа z, z =>* x.

Предложение – это сентенциальная форма, состоящая из терминальных символов.

Определение 7:

Язык L (G [ z ]) – это множество предложений:

L (G)={ x | z =>* x и x V_T ⁺ }.

Таким образом, язык – это просто подмножество множества всех терминальных цепочек, т.е. цепочек в V_T. Структура предложений задаётся грамматикой. Несколько различных грамматик могут порождать один и тот же язык.

Определение 8:

Пусть G [ z ] – грамматика. И пусть w = х U у – тогда u называется фразой сентенциальной формы w для нетерминального символа U, если z =>* xUу и U = u ⁺ (простая U => u).

Следует быть осторожным с терминалом фраза. Тот факт, что U = u ⁺ вовсе не означает, что u является фразой сентенциальной формы хuу, необходим z =>* xUу.

В качестве примера рассмотрим сентенциальную форму <пчс>1.

Значит ли, что <пчс> - является фразой, если существует правило <число>::=<пчс>? – нет, т.к. невозможно вывод <число>1 начального символа <число>. Имеет место вывод:

<число>=><пчс>=><пчс><цифра>=><пчс>1.

Таким образом:

<число>=>*<пчс> и <пчс>=>⁺<пчс>1

<число>=>*<пчс><цифра> и <цифра>=1

Тогда <пчс>1 и 1 фразы; 1 – простая фраза.

Определение 9:

Основой всякой сентенциальной формы называется самая левая простая фраза.

Грамматика G1 описывает бесконечный язык, т.к. существует правило <пчс>::=<пчс><цифра>.

В общем случае, если U =>⁺… U …, мы говорим, что грамматика рекурсивна. Если U =>+ U … то левая рекурсия, U =>⁺… U – правая.

Определение 10:

Если две различные грамматики порождают один и тот же язык, то эти грамматики называются эквивалентными.

Эквивалентные грамматики могут обладать разными свойствами, облегчающими или, наоборот, затрудняющими разработку алгоритма трансляции.

Каждой сентенциальной форме по определению соответствует, по крайней мере один вывод. Однако, одной и той же сентенциальной форме может соответствовать более, чем один вывод. Вывод можно наглядно представить синтаксическим деревом, которое иначе называют деревом вывода или деревом разбора. В качестве иллюстрации построим дерево вывода предложения - 75. 7.09.2005

Отправляясь от начального символа <число> нарисуем его куст, для того, чтобы указать первый непосредственный вывод:

Куст узла – это множество подчинённых узлов(символов), образующих цепочку, которая заметает имя куста, в непосредственном выводе. Концевые узлы не имеют подчинённого куста. Для второго вывода получаем:

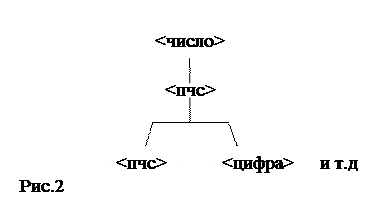
Строим три синтаксические диаграммы, каждый раз применяя непосредственный вывод.

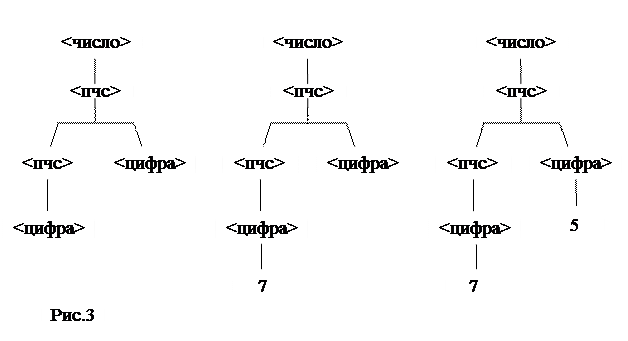
При чтении слева направо концевые узлы образуют цепочку, вывод которой представлен деревом. Можно восстановить вывод по синтаксическому дереву при помощи обработки процесса. Самый правый концевой указывает непосредственный вывод 7<цифра>=>75, чтобы пройти по синтаксическому дереву до куста 7<цифра> мы отсекаем куст от дерева – удаляем его. Продолжаем процесс всегда восстанавливая последний непосредственный вывод. Концевые узлы дерева образуют выводимую сентенциальную форму.

Определение 11:

Предложение грамматики неоднозначно, если для его вывода существует два синтаксических дерева. Грамматика неоднозначна, если она допускает неоднозначные предложения, в противном случае она однозначна.

Заметим, что мы называем неоднозначной грамматику, а не сам язык. Изменяя неоднозначную грамматику, но не заменяя её предложения, можно получить однозначную грамматику для того же множества предложений. Однако, есть языки для которых не существует однозначной грамматики. Такие языки называются существенно неоднозначными. Было доказано, что проблема распознавания неоднозначности алгоритмически не разрешима(т.е. не существует алгоритма, определяющего законченное число шагов однозначна или нет. Проблема Поста). Но можно разработать условие такие, что если грамматика удовлетворяет им, то она однозначна.

Пример:

{ a ⁱ b ⁱ c ^j|i,j ≥1}{ a ⁱ b ⁱ c ^j| i,j ≥1}

Задача разбора

Разбор сентенциальной формы означает построение вывода, и возможно, синтаксического дерева для неё. Программу разбора также называют распознавателем, т.к. она распознаёт только предложения рассматриваемой грамматики. (например, мы можем распознавать программы, написанные на языке программирования).

Мы рассмотрим алгоритмы разбора слева направо, того что они обрабатывают сначала самые левые символы рассматриваемой цепочки и продвигаются по цепочки направо, только тогда, когда это необходимо. Мы могли бы подобным же образом определить разбор справа налево, но он менее естественен.

Различают две категории алгоритмов разбора: нисходящий (сверху вниз) и восходящий (снизу вверх. Эти термины соответствуют способу построения синтаксических деревьев. При нисходящем разборе дерево строится от корня (начального символа) вниз к концевым узлам. Рассмотрим предложение 35 в следующей грамматике целых чисел.

На каждом последующем шаге самый левый элементарный символ V текущей сентенциальной формы xV y заменяется на правую часть правила V::= u, в результате получается следующая сентенциальная форма. Этот процесс для предложения 35 представлен в виде 5 деревьев. Требуется получить сентенциальную форму, которая совпадает с заданной цепочкой.

Метод восходящего разбора состоит в том, что отправляясь от заданной цепочки пытаются привести её к начальному символу. На первом шаге терминал 3 приводится к Д, в результате чего получается сентенциальная форма Д5.

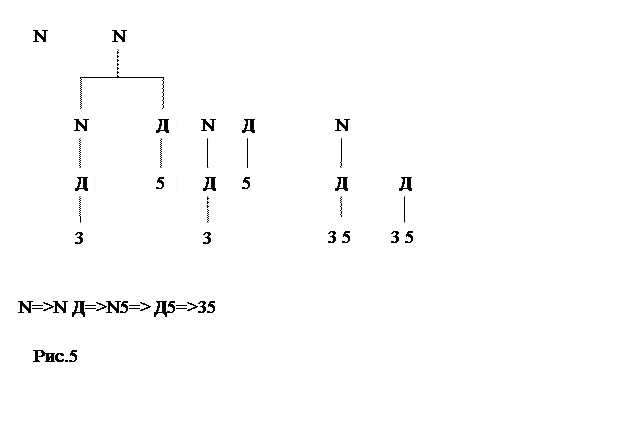
Выводы, произведённые двумя распознавателями, различны, но имеют одно и то же синтаксическое дерево. При разборе слева направо цепочка справа от основы всегда содержит только терминальные символы.

Определение 12:

Непосредственный вывод хUу => xuy называется каноническим и записывается хUу => xuy, если у содержит только терминалы.

Вывод W =>⁺ V называется каноническим и записывается W =>⁺ V, если каждый непосредственный вывод в нём является каноническим.

Классификация грамматик по Холмскому.

По Холмскому грамматика – это четвёрка (V, T, P, Z).

1. V – алфавит.

2. Т V - алфавит терминальных символов

3. Р – конечный набор правил постановки.

4. Z – начальный символ, который не является терминалом (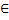 V – T)

Язык, порождаемый грамматикой, - это множество терминальных цепочек, которые можно вывести из Z.

Различие четырех типов грамматик заключается в форме правил подстановки, допустимых в Р.

Говорят, что G – это грамматика типа 0(по Холмскому) или грамматика с фазовой структурой, если правила имеют вид: u::= U, где u 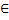V ⁺, U 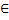V *, т.е. левая часть u может быть тоже последовательностью символов, а правая – пустой. Грамматики с фазовой структурой имеют небольшой употребление.

Если ввести ограничения на правила подстановки, то получится более интересный класс языков типа 1, называемых контекстно – зависимыми. Правила подстановки имеют вид:

xUу::= xuy, где U 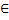V-T; u 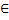V ⁺; x, y 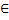V *

Термин контекстно-зависимые отражает тот факт, что можно заменить U на u в контексте х ….. у.

Дальнейшее ограничение правил подстановки даёт класс грамматик, называемых контекстно-свободные (КС) (все языки программирования описываются с помощью этой грамматики).

U::= u, где U 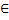V-T и u 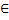V *

В КС – грамматиках может появится правило вида U::= λ.

По заданной КС – грамматике G можно сконструировать неукорачивающую грамматику типа G1 или λ – свободную, такую что L (G1)= L (G) – { λ } (тот же самый язык)

Если мы ограничим правила ещё раз, приведя их к виду U::= u или U::= WN, где N 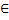T U, W 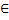V - T, то мы получим грамматику типа 3 или регулярную грамматику.

Из четырёх классов грамматик Холмского наиболее важным с точки зрения приложений к языку программирования является класс контекстно-свободных грамматик(или КС – грамматик). Это связано с тем, что средствами КС-грамматик удаётся достаточно полно описать синтаксические структуры существующих языков программирования, а так же с тем, имеются достаточно хорошо разработанные алгоритмы распознавания КС – языков, которые составляют важную часть транслятора - синтаксического анализа.

Рассмотрим использование регулярных грамматик. Они играют основную роль, как в теории языков, так и в теории автоматов. Множество цепочек, порождаемых регулярной грамматикой, допускается машиной называемой автоматом с конечным числом состояний и наоборот.

Большинство символов в языках программирования попадают в один из следующих классов: идентификаторы, служебные слова (подмножество идентификаторов), целые числа, однолитерные разделители (+, -, *,:=, и.т.д.). Эти символы могут быть описаны следующим простыми правилами:

<идентификатор>::= буква |<идентификатор>

буква |<идентификатор> цифра

<целое>::<цифра>|<целое> цифра

<разделитель>::=+|- | (|) | / |…

<разделитель>::=<SLASH>|<SLASH>*|<AST>*|

<COLON>=

<SLASH>::=/

<AST>::= *

<COLON>::=:

Правила могут быть ещё проще, но мы их записываем так, чтобы каждое правило имело вид U::= Т – левая часть терминал или U::= VT - левая часть начинается с нетерминала. Грамматики с такими правилами – регулярные грамматики.

Рассмотрим эффективный способ разбора предложений регулярной грамматики.

грамматики.

Дата добавления: 2014-01-11