
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Матрица предшествования
|
|
|
|
Отношение предшествования можно непосредственно найти, пользуясь определением. Однако, удобнее ввести дополнительное определение. Обозначим L(u) – множество самых левых символов относительно нетерминального символа U. Формально множество L(U) определяемая формулой L(U)={ S| 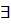 u=>*Sz},где z – ЛЮБАЯ строка, возможно пустая.
u=>*Sz},где z – ЛЮБАЯ строка, возможно пустая.
Или: L(u)={S| 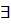 (U->Sz)v
(U->Sz)v 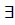 (U->U'z'^S
(U->U'z'^S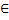 L(U '))}
L(U '))}
Аналогично обозначим R(u) – множество самых правых символов относительно нетерминального символа U. R(U)={ S| 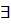 |U=>*zS}
|U=>*zS}
Или: R(U)={S| 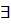 (U->zS)v
(U->zS)v 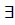 (U ->z'U'^S
(U ->z'U'^S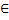 R(U'))}
R(U'))}
Эти 2 определения удобны для практического поиска множеств L(U) и R(U), которые используются для выявления отношений предшествования по следующим правилам:
1. Si 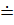 Sj ó
Sj ó 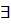 (U->xSiSjy) (1)
(U->xSiSjy) (1)
2. Si  Sj ó
Sj ó 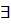 (U->xSiDy)^Sj
(U->xSiDy)^Sj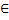 L(D) (2)
L(D) (2)
3. Si  Sj ó
Sj ó 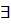 (U->xCSjy)^Si
(U->xCSjy)^Si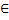 R(C)v
R(C)v 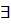 (U->xCDy)
(U->xCDy)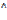 Si
Si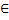 R (C)^Sj
R (C)^Sj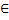 L(D) (3)
L(D) (3)
Здесь С и D нетерминальные символы, а х и у – цепочки, возможно пустые.
Пример1: Найти L(u) и R(u) для грамматики G1:
П -> В
В 
В-> T
B-> B+T
T->M (4)
T->TxM
M-> И
M-> (B)
Решение: нетерминальные символы грамматики G1: П, В, Т, М. Множества L(u) и R(u) нужно построить только для этих символов.
1. Для каждого нетерминального символа U находим все правила, содержащие U в левой части. В L(U) включается самый левый символ правой части каждого правила, а в R(U) – самый правый символ.
В результате получаем:
Множества L(u) и R(u) на 1 шаге:
| u | L(u) | R(u) |
| П В Т М | 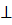 T, В
М, Т
И, (
T, В
М, Т
И, (
| 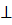 T
M
И,)
T
M
И,)
|
2. Просматривается каждое полученной множестве (см. рис.). Если множество L(u) содержит нетерминальные символы u',u'',…, то это множество дополняется символами, входящими в L(u'),L(u''),… и не входящими в L(u). Аналогичным образом дополняется множество R(u).
Имеем:
| u | L(u) | R(u) |
| П В Т М | 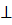 T,B,М
M,Т,И,(
И, (
T,B,М
M,Т,И,(
И, (
| 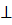 T,М
M,И,)
И,)
T,М
M,И,)
И,)
|
3. Выполнение шага 2 продолжается до тех пор, пока множества L(u) и R(u) не перестанут изменятся. В результате:
| u | L(u) | R(u) |
| П В Т М | 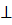 T,B,М,И,(
T,M,И,(
И, (
T,B,М,И,(
T,M,И,(
И, (
| 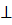 T,М,И,)
M,И,)
И,)
T,М,И,)
M,И,)
И,)
|
Окончательная таблица
Грамматика G1 не является грамматикой предшествования, т.к. из (1) и (4): ( 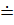 В (входят в основу и стоят рядом), +
В (входят в основу и стоят рядом), + 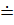 Т, а с другой стороны из (2) и (3), и таблицы => (
Т, а с другой стороны из (2) и (3), и таблицы => (  B и +
B и +  T, т.е. отношения предшествования для пар символов (, И и +Т неоднозначны.
T, т.е. отношения предшествования для пар символов (, И и +Т неоднозначны.
Неоднозначность отношений предшествования, встречаются в грамматиках языков программирования, в следствии того, что для выделении основы в методе предшествования используется минимальный контекст: сравниваются лишь пары символов. Для устранения неоднозначности, если она появляется, нужно либо изменить грамматику, либо использовать более далёкий контекст. Так, очевидно, в контексте (В) и В+Т+… справедливо соответственно: ( 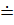 В и +
В и + 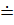 Т, поскольку возможны прямые редукции В к М и В+Т к В, то в контексте (В+Т) и … +ТхМ, напротив, справедливы отношения (
Т, поскольку возможны прямые редукции В к М и В+Т к В, то в контексте (В+Т) и … +ТхМ, напротив, справедливы отношения (  В и +
В и +  Т (ввиду того, что здесь нужно выполнить прямые редукции В+Т к В и ТхМ к Т).
Т (ввиду того, что здесь нужно выполнить прямые редукции В+Т к В и ТхМ к Т).
В данном конкретном случае формально неоднозначность отношений предшествования вытекает из того, что, с одной стороны символы (, В, а также + и Т встречаются в правых частях правил рядом, а с другой стороны B 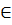 L(B) и T
L(B) и T 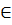 L(T). Если устранить рекурсивность множеств L(B) и L(T) относительно В и Т, то рассматривается грамматика станет грамматикой простого предшествования.
L(T). Если устранить рекурсивность множеств L(B) и L(T) относительно В и Т, то рассматривается грамматика станет грамматикой простого предшествования.
Заменим правила B->T и В->В+Т правилами
B->B'
B'->T
B'->B'+T,
и T->M., T->TxM правилами
T->T'
T'->M
T'->T'xM
Получим новую грамматику G' (эквивалентную):
П ->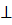 В
В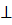
В-> B'
B'-> T
B'-> B'+T
T->T' (5)
T'->M
T'->T'xM
M-> И
M-> (B) – грамматика простого предшествования.
Отношения предшествования удобно записывать в виде матрицы предшествования, представляющей собой таблицу с двумя входами. Входами в таблицу являются предшествующий (Si) и последующий (Sj) символы приводимой строки, а в ее клетках записываются отношения предшествования.
Составим матрицу предшествования для грамматики G'1.
1 шаг Находим L(u) и R(u) по старому алгоритму.
| u | L(u) | R(u) |
| П В B' Т T' М | 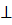 B',T,T',М, И,(
T, B', T', M, И,(
T’, M, И,(
M, И, (, Т'
И, (
B',T,T',М, И,(
T, B', T', M, И,(
T’, M, И,(
M, И, (, Т'
И, (
| 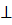 B',T,T',М, И,)
T, T', M, И,)
T, M, И,)
M, И,)
И,)
B',T,T',М, И,)
T, T', M, И,)
T, M, И,)
M, И,)
И,)
|
2 шаг Составляем матрицу предшествования.
i) Отношения 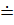 отыскиваем по (1) правилу непосредственных просмотром правых частей грамматики(4). Символы, стоящие в правой части рядом, связаны отношением
отыскиваем по (1) правилу непосредственных просмотром правых частей грамматики(4). Символы, стоящие в правой части рядом, связаны отношением 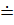 .
.
ii) Отношения  отыскиваем по правилу (2) путём просмотра правых частей порождающих грамматик G'1 с использованием таблицы, содержащей описания множеств L(D). Например, из правил T'->T'xM и L(M)={u,(} =>x
отыскиваем по правилу (2) путём просмотра правых частей порождающих грамматик G'1 с использованием таблицы, содержащей описания множеств L(D). Например, из правил T'->T'xM и L(M)={u,(} =>x  u и x
u и x  (.
(.
iii) Отношения  находим по правилу (3) путём просмотра правых частей G'1с использованием таблицы, содержащей описания множеств L(D) и R(C).
находим по правилу (3) путём просмотра правых частей G'1с использованием таблицы, содержащей описания множеств L(D) и R(C).
В результате выполнения этого алгоритма получается матрица предшествования.
| Sj Si | ( | И | M | x | T' | T | + | B' | ) | B |
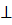
| |
| ) | 
| 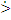
| 
| 
| ||||||||
| И | 
| 
| 
| 
| ||||||||
| M | 
| 
| 
| 
| ||||||||
| x | 
| 
| 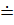
| |||||||||
| T' | 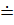
| 
| 
| 
| ||||||||
| T | 
| 
| 
| |||||||||
| + | 
| 
| 
| 
| 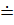
| |||||||
| B' | 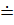
| 
| 
| |||||||||
| B | 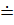
| 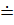
| ||||||||||
| ( | 
| 
| 
| 
| 
| 
| 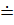
| |||||
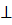
| 
| 
| 
| 
| 
| 
| 
|
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 2644; Нарушение авторских прав?; Мы поможем в написании вашей работы!