Основные понятия и определения. Условия геометрической неизменяемости стержневых систем

Условия геометрической неизменяемости стержневых систем.

Начинать расчёт сооружения имеет смысл лишь тогда, когда установлено, что он вообще может быть выполнен методами строительной механики, и определено, какие методы при этом следует использовать. В противном случае попытки составить и решить соответствующие уравнения могут оказаться безуспешными из-за возникновения нехарактерных для решаемой задачи математических проблем (недостаточность уравнений, их вырождение и др.). Поэтому необходима предшествующая расчёту оценка расчётной схемы рассматриваемой системы, называемая кинематическим анализом сооружения (системы).

К и н е м а т и ч е с к и й а н а л и з – это исследование расчётной схемы сооружения (системы), выполняемое до на­чала расчёта с целью определения кинематического качества системы (геометрической неизменяемости, мгновенной изме­няемости или геометрической изменяемости), а в случае гео­метрической неизменяемости системы – также для выявления её статической определимости или неопределимости.

Кинематический анализ позволяет своевременно обнаружить системы, расчёт которых либо вообще невозможен методами механики деформируемых тел – геометрически изменяемые системы (ГИС), либо может выполняться с использованием особых подходов – системы мгновенно изменяемые (МИС). Кроме того, в результате кинематического анализа выясняется, как именно предстоит рассчитывать систему – достаточно ли для определения усилий в системе одних только уравнений статики (в случае статически определимой системы) или необходимо рассматривать все три стороны задачи расчёта деформируемой системы – статическую, геометрическую и физическую (если система статически неопределимая).

Принципиальная схема кинематического анализа приведена на рис.1.6. Методика и техника выполнения проверок, обозначенных на блок-схеме операторами 1, 2 и 3, будут рассмотрены далее. Формально процедуры, описанные в правой части схемы, могут и не выполняться, если не ставить задачу добиться всё-таки возможности выполнить расчёт сооружения – либо путем трансформации расчётной схемы, либо – для мгновенно изменяемой системы – выбором специальных методов расчёта.

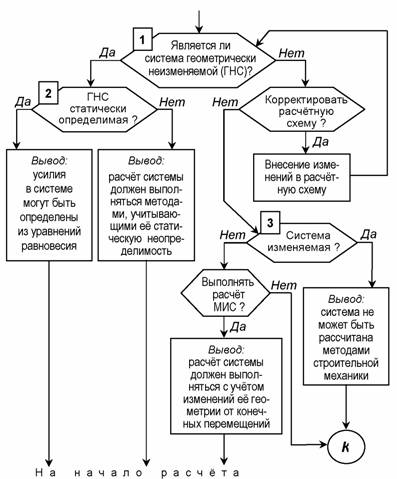
Рис.1.6

Строительная механика рассматривает геометрически неизменяемые системы (сооружения), то есть такие, перемещения точек которых возможны только в результате деформации системы.

Наипростейшей неизменяемой системой является шарнирный треугольник (рис.1.7).

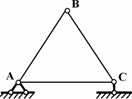
Рис.1.7

Шарнирно-стержневой прямоугольник АВСД, показанный на рис.1.8, является геометрически изменяемой системой, так как приходит в движение без изменения длины и искривления стержней даже при бесконечно малых нагрузках.

Рис.1.8

Кроме уже известных понятий «геометрическая неизменяемость» (и соответственно геометрически неизменяемая система – ГНС), «геометрическая изменяемость» (геометрически изменяемая система – ГИС), «мгновенная изменяемость» (мгновенно изменяемая система – МИС), базовыми понятиями кинематического анализа являются диск, связь и степень свободы.

Д и с к – часть системы (один или несколько соединённых друг с другом элементов), форма и размеры которой могут изменяться только вследствие деформации материала.

Иными словами, если использовать гипотезу отвердения материала (считать материал недеформируемым), то признаком диска будет неизменность формы и размеров.

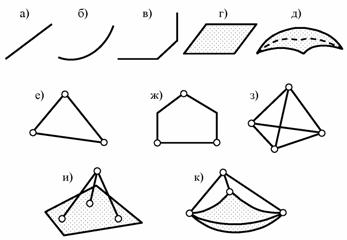
Рис. 1.9

Примеры дисков приведены на рис. 1.9:

– а, б, в, г, д – диски из одного элемента (а, б, в – стержни с прямолинейной, криволинейной и ломанной в плоскости или в пространстве осью; г – диск-пластинка; д – диск-оболочка);

– е, ж, з, и, к – диски из нескольких элементов (е, ж, з – из однотипных элементов – стержней, плоские (е, ж) и пространственный (з); и, к – комбинированные пластинчато- и оболочечно-стержневые, пространственные).

Незакреплённый диск может перемещаться в плоскости или пространстве, при этом координаты его точек в общей (глобальной) системе координат xyz изменяются (рис. 1.10), но в собственных (локальных) координатных осях x_D y_D z_D, связанных с самим диском, положение его точек остается неизменным, если считать элементы диска недеформируемыми, – это означает, что диск перемещается как жёсткое целое.

Рис. 1.10

Диск может быть образован соединением нескольких ранее выявленных дисков, имеющих любую (возможно, достаточно сложную) внутреннюю структуру. Пример – на рис. 1.11, где в состав плоского диска I (D _I) входят многостержневые «суб»-диски 1, 2 и 3 (D ₁ , D ₂ и D ₃), объединённые в шарнирный треугольник аналогично примерам на рис. 1.9, е, ж. Неизменяемость формы шарнирного треугольника очевидна; в дальнейшем будет дано доказательство этого.

Рис.1.11

Поскольку возможно последовательное «укрупнение» дисков, то ясно, что в ряде случаев (но не всегда!) вся система может рассматриваться, в конечном счете, как диск.

Особым диском, который используется в кинематическом анализе, является диск «земля», представляющий собой единую модель всех реальных объектов, играющих роль основания для рассчитываемого сооружения, – фундаментов, других конструкций, поддерживающих рассматриваемую систему.

Диск «земля» всегда считается неподвижным и недеформируемым (возможная деформативность реального основания изначально закладывается в расчётную схему сооружения путем введения податливых опор).

Для обеспечения геометрической неизменяемости сооружения его элементы и более крупные фрагменты (по терминологии кинематического анализа – диски) должны быть соединены (связаны) друг с другом и хотя бы некоторые из них – обязательно с «землей». Соответствующие соединительные устройства принято называть связями. Более общее определение связей объединяет их механико-математическое и прикладное (инженерное) истолкования:

с в я з и (механические) – ограничения на перемещения (линейные и/или угловые) точек или сечений элементов системы, а также устройства, технически реализующие эти ограничения.

З а м е ч а н и е: здесь термин «сечение элемента» не означает разделения элемента на части, а используется в том же смысле,

как в общепринятых выражениях «гипотеза плоских сечений», «угол поворота сечения», т.е. как указание на геометрический объект, для которого определяются или описываются кинематические свойства или параметры, в частности, перемещения.

Ограничения (одно или одновременно несколько) перемещений точки или сечения возникают в том случае, когда эта точка (сечение) некоторым способом соединяется с другими точками (сечениями элементов) одного и того же или разных дисков, в том числе диска «земля».

Абстрагируясь от конструктивных особенностей соединительных устройств, будем рассматривать их расчётные модели, применяя к ним в дальнейшем термин «связи».

Дата добавления: 2014-01-11