Теорема о взаимности перемещений

По-прежнему рассмотрим состояния i и j одного и того же сооружения (рис. 6.11). В состоянии i на него действует сила F_i = 1, а в состоянии j – сила F_j = 1. Зафиксируем возможные перемещения и , возникающие в состояниях i и j от единичных сил.

Для состояний сооружения i и j применим теорему о взаимности возможных работ внешних сил (см. соотношение (6.3)):

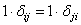, или . (6.4)

Соотношение (6.4) выражает содержание теоремы о взаимности перемещений: перемещение по направлению линии действия i-й единичной обобщённой силы, вызванное j-й единичной обобщённой силой, равно перемещению по направлению линии действия j-й обобщённой силы от i-й единичной обобщённой силы. В строительной механике эта теорема известна как теорема английского физика и механика Джеймса Максвелла (1831–1879).

Рис.6.11

Теорема о взаимности перемещений широко применяется в расчётах линейно деформируемых систем, в частности, в расчётах статически неопределимых систем методом сил, при построении линий влияния перемещений в стержневых сооружениях.

Выше был рассмотрен случай, когда в состоянии i и j сооружения действуют единичные сосредоточенные силы (рис. 6.11), т.е. силы, имеющие одинаковую природу и одинаковую размерность. На рис. 6.12 рассмотрена ситуация, когда в состоянии i на сооружение действует сосредоточенная сила F_i = 1, а состоянии j – сосредоточенный момент M_j = 1. Здесь же показаны и возможные перемещения и , вызываемые упомянутыми силами F_i = 1 и M_j = 1. Кажущееся противоречие в размерностях перемещений и , равенство которых определено соотношением (6.4), отпадает, если мы примем во внимание, что каждое из этих перемещений является удельным перемещением, т.е. что оно вызывается обобщённой силой, имеющей не произвольное, а единичное значение. Таким образом, размерность какого-либо удельного перемещения есть отношение размерности рассматриваемого обобщённого перемещения к размерности обобщённой силы, вызвавшей это перемещение. В случае, рассмотренном на рис. 6.12, имеем:

= см/кНсм = кН^-1, 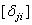= рад/кН = кН^-1,

т.е. оба перемещения имеют одинаковую размерность.

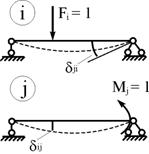
Рис.6.12

Дата добавления: 2014-01-11