Определение мест расположения региональных дистрибьюторов

После определения каналов распределения продукции и услуг необходимо выявить места их расположения. Наукой и практикой выработаны следующие методы решения данной проблемы:

Метод полного перебора. Задача выбора оптимального расположения торговых посредников решается полным перебором и оценкой всех возможных вариантов их размещения и выполняется на ЭВМ методами математического программирования.

Эвристические методы. При использовании данных методов анализируется транспортная сеть внутри зоны потенциального сбыта продукции (ЗПСПУ - под которой понимается определенная часть географической территории, находящейся в сфере маркетинговых интересов предприятия-поставщика и охватывающей места расположения потенциальных потребителей реализуемой им продукции, которые могут иметь экономическую или иную выгоду от ее приобретения у данного предприятия по сравнению с альтернативными вариантами ее покупки у конкурирующих предприятий) регионального дистрибьютора и отбраковываются непригодные с точки рения специалиста варианты. Т.о., проблема выбора упрощается до разумного числа альтернатив, которые необходимо оценить с применением ЭВМ;

Метод весового (или локационного) треугольника В. Лаунхардта.

Суть этого метода заключается в следующем:

Пусть требуется найти пункт размещения нового металлургического завода. Известны пункты добычи железной руды – точка А (рис. 1.), пункт добычи угля – точка В и пункт потребления металла – точка С. Расход руды на выплавку 1 т металла равен а, расход угля – b. Известны также расстояния между пунктами (стороны локационного треугольника): AC=S₁, BC=S₂, AB=S₃.

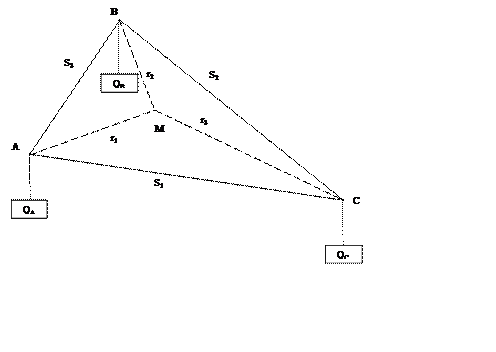
Рис. 1. Локационный треугольник В. Лаухнардта

Возможным пунктом размещения завода может быть каждая из трех точек размещения источников руды и угля, а также потребителя металла. В этих случаях суммарные затраты, связанные с перевозкой необходимых грузов для потребления тонны металла, будут равны:

(bS₃+S₁)p – при размещении завода в точке А;

(aS₃+S₂)p – при размещении завода в точке В;

(aS₁+bS₂)p – при размещении завода в точке С, где р – транспортный тариф.

Наилучшим пунктом размещения завода из рассмотренных трех пунктов будет тот, в котором транспортные затраты будут минимальны. Однако искомый пункт размещения может не совпадать ни с одной из вершин локационного треугольника, а находится внутри него в некоторой точке М.

Расстояние от внутренней точки М до вершин треугольника составляет АМ=r₁, BM=r₂, CM=r₃. Тогда транспортные издержки при размещении металлургического завода в точке М будут равны:

Выполнение требования Т→min дает точку оптимального места расположения предприятия.

Данная задача имеет геометрическое и механическое решение. Геометрический метод нахождения точки размещения состоит в том, что на каждой из сторон локационного треугольника строится треугольник, подобный весовому (стороны которого относятся как а:b:1). Затем вокруг построенных таким образом треугольников описывают окружности, точка пересечения которых является точкой минимума транспортных затрат. Этот метод применим для случая, когда соотношения расстояний S₁, S₂, S₃ соответствуют свойству треугольника (одна сторона меньше трех других). В противном случае (например, когда S₁>S₂+S₃) точка минимума транспортных затрат будет совпадать с одной из вершин локационного треугольника.

Механическое решение рассматриваемой задачи основывается на аналогии с методом нахождения точки равновесия сил. При этом вес руды, угля, металла выступает в качестве сил, с которыми «притягивают» производство соответствующие вершины локационного треугольника. Искомая точка является точкой равновесия трех связанных нитей, проходящих через вершины локационного треугольника. При этом к концам нитей подвешены грузы (Q_A, Q_B, Q_C)? пропорциональные a, b, 1.

Рассмотрим один из подходов к решению поставленной проблемы. Центр тяжести системы, или центр массы, может быть определен по формуле:

М – центр массы, км;

R_nj – расстояние от начала осей координат до точки, обозначающей место расположения клиента, км;

R_ki – расстояние от начала координат до точки, обозначающей место расположения потребителя, км;

T_nj – транспортный тариф для поставщика на перевозку груза, руб./ткм;

T_ki – транспортный тариф для клиента на перевозку груза, руб./ткм;

Q_nj – объем груза, закупаемый у j-го поставщика, т;

Q_ki – объем груза, реализуемый i –му клиенту, т.

Дата добавления: 2014-01-11