Элементарная теория пар сил

Парой сил называется система двух равных по модулю параллельных сил, направленных в противоположные стороны (см. рисунок 16,а, где по модулю F = F₁).

Сумма сил (равнодействующая) пары равна нулю, но пара сил не уравновешена, т. к. пара стремится повернуть тело, к которому она приложена, в соответствующем направлении.

Кратчайшее расстояние между линиями действия сил пары называется плечом пары сил h. Плоскость, в которой действуют силы пары, называется плоскостью действия пары сил. Действие пары на твердое тело сводится к вращательному эффекту, мерой которого является векторная величина 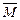(см. рисунки 16,а и 16,б), называемая моментом пары сил. Вектор пары 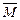направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.

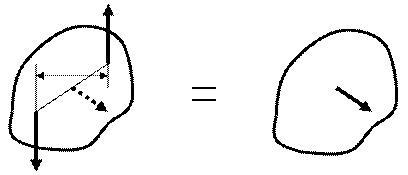
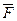
h В

О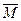

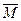
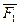
а) б)

Рисунок 16. Пара сил, момент пары сил: а) исходная схема; б) эквивалентная схема

Модуль этого вектора равен произведению модуля силы 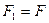пары на ее плечо 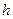: 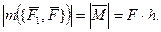(8)

Совокупность нескольких пар сил, действующих на тело, называется системой пар сил. Пара сил не приводится к равнодействующей (ее равнодействующая равна нулю).

В отличие от момента силы относительно точки 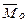вектор пары сил 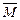является свободным вектором, т. е. его можно приложить в любой точке тела.

Основные свойства пары сил:

- пару сил можно переносить куда угодно в плоскости действия пары;

- пару можно переносить из данной плоскости в любую плоскость, параллельную данной;

- у данной пары можно произвольно менять модули сил и длину плеча, сохраняя неизменным ее момент.

Пары сил эквивалентны, если равны векторы-моменты этих пар.

Легко доказывается, что момент пары сил равен сумме моментов относительно любой точки О сил, образующих пару.

Если на тело действует несколько (n) пар с моментами 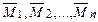, то их совокупное воздействие на тело эквивалентно одной паре с моментом

.

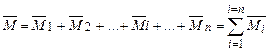ГЛОССАРИЙ

Нүктеге қатысты күш моментi	Момент силы относительно точки	Moment of force about point
Өске қатысты күш моментi	Момент силы относительно оси	Moment of force about axis
Күш иiнi	Плечо силы	Moment arm
Қос күш	Пара сил	Couple
Қос күш иiнi	Плечо пары	Arm of couple
Қос күш моментi	Момент пары	Moment of couple

Рекомендуемая литература

1. Тарг С.М. Краткий курс теоретической механики: Учеб для втузов. – М.: Высш. шк., 1986 (и последующие издания). – 416 с.:

- с. 18…24 – операции с силами, равновесие системы сходящихся сил, решение задач;

- с. 31…37 – моменты сил, пары сил; с. 72…75 – моменты сил относительно оси.

2. Молотников В.Я. Основы теоретической механики/Серия «Высшее образование». – Ростов н/Д: «Феникс», 2004. – 384 с.:

- с. 13…16 – силы, системы сил;

- с. 24…31 – основы векторной алгебры;

- с. 31…39 – равновесие системы сходящихся сил,

- с. 43…52 – моменты сил, пары сил).

Контрольные задания для СРС:

1) Будут ли эквивалентны силы, если равны их моменты: а) относительно одного центра; б) относительно любого центра?

2) Могут ли быть равными моменты двух различных сил относительно одной и той же точки?

3) Доказать самостоятельно свойство пары сил о переносе ее в параллельную плоскость.

4) Самостоятельно получите аналитическое выражение момента силы относительно оси у: 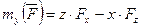, изобразив соответствующую схему, подобную схемам на рисунке 15.

5) Доказать, что момент пары сил равен сумме моментов относительно любой точки О сил, образующих пару.

Дата добавления: 2014-01-11