Общее и аналитические условия равновесия произвольной системы сил (плоской и пространственной)

Из теоремы о приведении системы сил к силе и паре сил, можно вывести условия равновесия системы сил, действующих на твердое тело. Для равновесия системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен нулю и главный момент системы сил относительно любого центра приведения также был равен нулю, т.е.

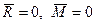. (10)

Эти условия являются векторными (общими) условиями равновесия для любой системы сил.

Аналитически главный вектор и главный момент системы сил определяются своими проекциями на координатные оси. Поэтому можно записать условия равновесия (6 уравнений) произвольной пространственной системы сил в аналитической форме:

(11)

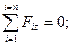
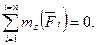
Условия (аналитические уравнения) равновесия произвольной плоской системы сил (три варианта совокупности уравнений):

1)

основной – классический комплект уравнений;

(12)

2)

точки О, В, С не должны лежать на одной прямой;

(13)

3)

(14)

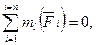ось l не должна быть перпендикулярна О В.

ГЛОССАРИЙ

Күштер жүйесiнiң бас векторы	Главный вектор системы сил	Resultant of system of force
Күштер жүйесінiң бас моменті	Главный момент системы сил	Moment of system of force about point
Күштер жүйесiн берiлген центрге келтiру	Приведение системы сил к заданному центру	Reduction of system of force
Теңдестiрiлген күштер жүйесi	Уравновешенная система сил	Balanced system of force
Күштер жүйесiнiң тепе-теңдiгi	Равновесие системы сил	Equilibrium of system of force

Рекомендуемая литература

1. Тарг С.М. Краткий курс теоретической механики: Учеб для втузов. – М.: Высш. шк., 1986 (и последующие издания). – 416 с. (с. 37…41; с. 44…48 – приведение системы сил к точке, общие условия равновесия сил, решение задач; с. 79…86 – равновесие пространственной системы сил, решение задач).

2. Молотников В.Я. Основы теоретической механики/Серия «Высшее образование». – Ростов н/Д: «Феникс», 2004. – 384 с. (с. 52…56 – теорема о параллельном переносе силы; с. 56…60; с. 64…68 – условия равновесия произвольной системы сил; с. 61…64 – теорема о приведении заданной системы сил к произвольной точке).

Контрольные задания для СРС:

1) получить условия равновесия системы параллельных сил (для плоской системы сил, для пространственной системы сил);

2) выясните, в каком случае центр тяжести тела обязательно совпадает с центром тяжести его объема и когда эти центры могут не совпадать;

3) определите положение центра тяжести произвольного сектора круга, сегмента круга и четверти окружности;

4) с помощью учебников выяснить, почему в варианте 2 совокупности уравнений равновесия произвольной плоской системы сил точки О, В, С не должны лежать на одной прямой?

5) почему в варианте 3 совокупности уравнений равновесия произвольной плоской системы сил ось l не должна быть перпендикулярна ОВ?

часть 2 «Сопротивление материалов»

Дата добавления: 2014-01-11