Внутренние усилия в стержнях при центральном растяжении-сжатии, применение метода сечений

Общие положения по теме

План лекции

1. Внутренние усилия в стержнях при центральном растяжении-сжатии, применение метода сечений.

2. Эпюры внутренних усилий при центральном растяжении-сжатии стержней.

Центральное растяжение-сжатие прямых жестких стержней – самый простой вид силового воздействия на элементы конструкций типа прямых стержней, при котором равнодействующие внешних нагрузок прикладываются к стержням вдоль их центральной оси. Центральная ось стержня – это воображаемая линия, которая проходит через точки, являющиеся центрами тяжести площадей всех его поперечных сечений. Поперечное сечение стержня – это воображаемая плоская фигура, которая получается, если мысленно рассечь стержень плоскостью поперек его центральной продольной оси. Простейшим примером центрального растяжения стержней являются канаты грузоподъемных машин, примером центрального сжатия – шток или винт гидравлического или винтового домкратов, применяемых для подъема грузов на небольшую высоту. В данной теме жесткость стержней, которые при работе в конструкции подвергаются только растяжению, не ограничивается. Жесткость же стержней, работающих на сжатие или на растяжение-сжатие, считается достаточно большой, чтобы при сжатии внешними нагрузками не возникало потери устойчивости, т. е. их изгибного искривления (выпучивания). Центральное сжатие нежестких стержней рассматривается отдельно в теме «Устойчивость центрально сжатых стержней», где учитывается понятие «гибкость» стержня.

Следует отметить, что растяжение и/или сжатие стержней бывает также внецентренным, когда равнодействующие внешних сил передаются на стержни параллельно их центральной оси со смещением (с эксцентриситетом) относительно нее. Такое силовое воздействие является более сложным, нежели рассматриваемое здесь центральное растяжение-сжатие прямых стержней, и рассматривается оно позднее в разделе «Сложное сопротивление стержней».

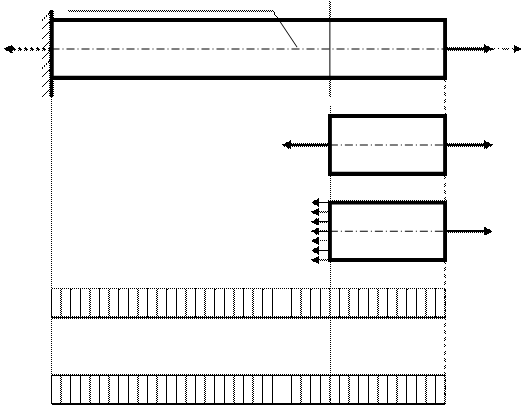
Рассмотрим простейший случай нагружения стержня – центральное его растяжение внешней силой F, cм. рисунок 24,а. Другие нагрузки, например, собственную силу тяжести стержня, в данном случае учитывать не будем. Внешнюю силу F считаем сосредоточенной силой, приложенной в точке пересечения центральной оси z стержня с правым его торцевым сечением. Следует отметить, что реально в точке (размеры которой бесконечно малы) приложить силу к телу невозможно. Однако нередко сосредоточенные силы можно без заметного ущерба для точности инженерных расчетов считать приложенными к элементу

конструкции в точке. Согласно принципу французского ученого Сен-Венана (1797-1886) способ концентрированного приложения к данному телу внешних сил существенно влияет на распределение внутренних сил только вблизи мест нагружения, т. е. неравномерность распределения внутренних сил в данном теле при передаче на него нагрузки от другого тела через небольшую площадку носит местный (локальный) характер. По мере удаления от мест концентрированных силовых воздействий неравномерность распределения внутренних сил быстро затухает. В данном случае неравномерность распределения внутренних сил в локальной зоне, непосредственно примыкающей к точке действия силы F принимать во внимание не будем. Примем, что распределение внутренних усилий в стержне зависит только от величины равнодействующей силы F, приложенной в точке его центральной оси z.

Центральная ось стержня n

а)

R F z

n

N F

б)

σ F

в)

г) 15 + 15 Эпюра N

(кН)

д) 100 + 100 Эпюра σ

(МПа)

Рисунок 24. Применение метода сечений для определения внутренних усилий и построения эпюр внутренних усилий в стержнях при центральном растяжении-сжатии (значения внутренних усилий N и σ на эпюрах соответствуют внешней силе F = 15 кН и площади сечения A = 150 мм² при А = const по всей длине стержня).

Для определения внутренних усилий в элементах конструкций при действии на них внешних нагрузок применяется метод сечений. Рассмотрим его применение к данному конкретному случаю центрального растяжения стержня. Сразу отметим, что стержень в целом находится в состоянии статического равновесия под действием заданной внешней

силы F и силы реакции опоры R = F. В том месте стержня, в котором надо определить внутреннее усилие мысленно проводим сечение n-n (рассекаем стержень). При этом мысленно представим, что стержень состоит из множества продольных «волокон» (стерженьков с бесконечно малым поперечным сечением), которые удлиняются одинаково и, следовательно, все поперечные сечения рассматриваемого стержня перемещаются параллельно их начальным положениям.

Такая картина деформации стержня соответствует гипотезе плоских сечений (гипотезе плоских сечений Я. Бернулли: поперечные сечения стержня, плоские и перпендикулярные его продольной центральной оси до деформации, остаются плоскими и перпендикулярными этой оси и после деформации). Далее следует отбросить из рассмотрения любую часть рассеченного стержня (в данном случае отбросим левую часть стержня относительно сечения n-n). Так как стержень в целом находится в силовом равновесии, то и каждая из его частей также находится в статическом равновесии. Отбрасывание одной из частей стержня необходимо эквивалентно заменить приложением в центре сечения такой системы внутренних сил, которая уравновесит действие на нее внешних сил. Рассмотрим равновесия правой части стержня, см. рисунок 24,б. На нее действует заданная сила F и в сечении n-n должна возникать такая система сил, которая обеспечит уравновешивание этой части стержня, т. е. эквивалентно заменит отбрасывание левой части стержня. Очевидно, что в данном простом случае для равновесия правой части стержня в центре сечения n-n должно возникать только одно внутреннее усилие, обозначенное через N и направленное в сторону, противоположную F. В дальнейшем силу N будем называть внутренней продольной силой. Остается определить значение этой внутренней продольной силы N. Очевидно, что N = F. Более строго для определения внутренних усилий в сечении стержня следует применять уравнения статического равновесия рассматриваемой части стержня. В данном случае для описания равновесия правой части стержня достаточно применить одно уравнение (сумма проекций всех сил на ось z должна быть равна нулю): 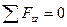или 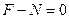, откуда .

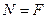Правило знаков для внутренней продольной силы N следующее: если сила N действует на рассматриваемую часть стержня растягивающим образом, т. е. в направлении от сечения, то такая сила N считается положительной (знак +), если же сила N реально действует сжимающим образом, т. е. в направлении к сечению, то такая сила N считается отрицательной и в инженерных расчетах ее значение учитывается со знаком – (минус).

Описанную процедуру применения метода сечений для определения внутренних усилий в учебной литературе иногда дополняют простой для запоминания аббревиатурой РОЗУ, в которой каждая буква является первой буквой ключевого слова четырех операций метода сечений: Р – рассечение стержня плоским сечением в том его месте, где надо определить внутренние усилия; О – отбрасывание одной из частей стержня относительно проведенного сечения; З – замена отброшенной части стержня уравновешивающей системой сил, приложенных в центре выполненного сечения; У – уравновешивание, т. е. применение уравнений статического равновесия для определения значений внутренних усилий в данном сечении стержня.

Внутренняя продольная сила N фактически распределена по площади А поперечного сечения n-n и является равнодействующей этого распределенного усилия, которое принято называть нормальным напряжением σ (нормальным потому, что оно по отношению к плоскости сечения n-n направлено нормально). Для многих случаев центрального растяжения-сжатия стержней на основании гипотезы плоских сечений Бернулли можно принять, что все продольные «волокна» материала деформируются одинаково, поэтому нормальное напряжение σ можно принять равномерно распределенным по площади А сечения (см. рисунок 24,в) и определять по формуле

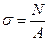и 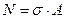, где σ = const по площади А. (15)

В тех случаях, когда нормальное напряжение σ распределено по площади поперечного сечения А неравномерно (такие случаи рассматриваются в других разделах курса), необходимо знать закон его распределения σ = σ(А) по площади А. Тогда внутреннюю продольную силу следует определять по формуле

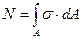. (16)

Базовой единицей измерения нормального напряжения σ является Паскаль: 1 Па = 1 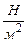; часто в расчетах применяется мегапаскаль – МПа (причем 1 МПа = 10⁶ Па) или килопаскаль кПа (1 кПа = 10³ Па); для некоторых расчетов полезно знать, что численно 1 МПа = 1 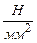(Ньютон на квадратный миллиметр); иногда в промежуточных расчетах удобно применять единицы измерения напряжения 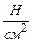(Ньютон на квадратный сантиметр).

Дата добавления: 2014-01-11