Условия статической прочности стержней при центральном растяжении и сжатии

Расчетная оценка прочности элементов конструкций является одной из важнейших инженерных задач, которые приходится решать при проектировании различных конструкций. После определения с помощью метода сечений внутренних усилий и напряжений в опасных (наиболее напряженных) поперечных сечениях центрально растянутого (или сжатого) стержня и выбора допускаемого напряжения 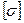(расчетного сопротивления R, умноженного на коэффициент условий работы строительной конструкции γ) можно провести оценку его прочности. 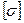Для этого расчетное напряжение в расчетном сечении стержня сопоставляется с допускаемым напряжением (или 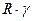), что обычно записывается в форме проверочного условия прочности стержней при центральном растяжении-сжатии:

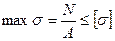или , (23)

где N – внутренняя продольная сила в расчетном сечении стержня, найденная с помощью метода сечений;

А – площадь расчетного сечения стержня.

Пользуются этим условием при проверочных расчетах прочности следующим образом. Если расчетное значение напряжения max σ не превышает допускаемого напряжения 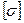(или 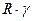), то считается, что статическая прочность стержневого элемента конструкции при центральном растяжении (сжатии) достаточна. Вместе с тем, у инженеров-проектировщиков есть неофициальное соглашение о том, чтобы считать статическую прочность конструкций достаточной также при небольшом (до 5%) превышении расчетного напряжения max σ над допускаемым 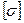(или 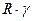): это не приведет к сколько-нибудь заметному снижению надежности конструкции по критерию статической прочности. Если же расчетное значение напряжения max σ превышает допускаемое напряжение 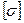(или 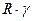) более чем на 5%, то считается, что статическая прочность стержневого элемента конструкции при центральном растяжении (сжатии) недостаточна и необходимо скорректировать (изменить) конструктивно-технологические параметры конструкции (стержня) с целью достижения условия прочности. При этом возможны следующие варианты корректировки:

- конструктивные изменения (например, изменить конструкцию расчетных сечений стержня так, чтобы увеличилась расчетная площадь сечения А и соответственно уменьшилось расчетное напряжение max σ);

- технологические изменения (например, можно применить для конструкции материал с более высокими характеристиками прочности, т. е. с более высоким допускаемым напряжением 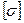или 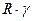; можно также применить механические, термические, химико-термические и другие технологические методы упрочнения материала, повышающие его прочностные характеристики);

- конструктивно-технологические изменения.

Вышеприведенное условие статической прочности элементов конструкций при центральном растяжении-сжатии можно преобразовать для использования при проектировочных расчетах, т. е. для определения требуемого прочного размера (площади) сечения (проектировочное условие прочности):

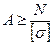или 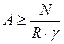. (24)

На основе вышеприведенного условия статической прочности можно также (по известным значениям продольного усилия N и допускаемого напряжения 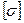или 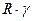) определить допускаемую продольную силу:

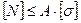или 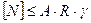. (25)

Дата добавления: 2014-01-11