
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекции по ТЭЦ
|
|
|
|
План счетов бухгалтерского учета, его основные разделы
Счета синтетического и аналитического учета. Взаимосвязи между счетами синтетического и аналитического учета
Для получения разных по степени детализации показателей в бухгалтерском учете используются синтетические и аналитические счета.
Синтетические счета содержат обобщенные данные о хозяйственных операциях и ведутся в денежном выражении. Однако, имея только общие показатели, нельзя осуществлять оперативное руководство, контроль и анализ хозяйственной деятельности. Для этого необходимы более детальные сведения, характеризующие состояние и движение каждого объекта учета – такие сведения обеспечивают аналитические счета.
Отражение объектов бухгалтерского учета в денежном выражении на синтетических счетах называется синтетическим учетом, их детализированное отражение на аналитических счетах называется аналитическим учетом.
Между счетами аналитического и синтетического счета существует взаимосвязь:
· начальный и конечный остатки синтетического счета должны быть равны общим суммам соответствующих остатков аналитических счетов;
· обороты по дебету и кредиту синтетического счета должны быть равны соответствующим итогам оборотов по аналитическим счетам.
План счетов утвержден приказом Минфина РФ от 31 октября 2000 г. N 94н (в редакции от 08.11.2010). План счетов применяется в организациях (кроме кредитных и государственных (муниципальных) учреждений) всех форм собственности и организационно-правовых форм, ведущих учет методом двойной записи.
План счетов представляет собой схему регистрации и группировки фактов хозяйственной деятельности в бухгалтерском учете. В нем приведены наименования и номера синтетических счетов (счетов первого порядка) и субсчетов (счетов второго порядка).
На основе данного Плана счетов организации утверждают рабочий план счетов бухгалтерского учета, содержащий полный перечень синтетических и аналитических счетов, необходимых для ведения бухгалтерского учета. В соответствии с действующей инструкцией все счета плана счетов сгруппированы по девяти основным разделам:
· Раздел I - Внеоборотные активы (01-09). Счета этого раздела плана счетов предназначены для обобщения информации о наличии и движении активов организации, которые в соответствии с правилами бухгалтерского учета относятся к основным средствам, нематериальным активам и другим внеоборотным активам, а также операций, связанных с их строительством, приобретением и выбытием.
· Раздел II - Производственные запасы (10-19). Счета этого раздела плана счетов предназначены для обобщения информации о наличии и движении предметов труда, предназначенных для обработки, переработки или использования в производстве либо для хозяйственных нужд, средств труда, которые в соответствии с установленным порядком включаются в состав средств в обороте, а также операций, связанных с их заготовлением (приобретением).
· Раздел III - Затраты на производство (20-29). Счета этого раздела плана счетов предназначены для обобщения информации о наличии и движении предметов труда, предназначенных для обработки, переработки или использования в производстве либо для хозяйственных нужд, средств труда, которые в соответствии с установленным порядком включаются в состав средств в обороте, а также операций, связанных с их заготовлением (приобретением).
· Раздел IV - Готовая продукция и товары (40-46). Счета этого раздела предназначены для обобщения информации о наличии и движении готовой продукции (продуктов производства) и товаров.
· Раздел V - Денежные средства (50-59). Счета этого раздела предназначены для обобщения информации о наличии и движении денежных средств в российской и иностранных валютах, находящихся в кассе, на расчетных, валютных и других счетах, открытых в кредитных организациях на территории страны и за ее пределами, а также ценных бумаг, платежных и денежных документов.
· Раздел VI - Расчеты (60-79). Счета этого раздела плана предназначены для обобщения информации о всех видах расчетов организации с различными юридическими и физическими лицами, а также внутрихозяйственных расчетов.
· Раздел VII - Капитал (80-86). Счета этого раздела предназначены для обобщения информации о состоянии и движении капитала организации.
· Раздел VIII - Финансовые результаты (90-99). Счета, входящие в этот раздел плана, служат для обобщения информации о доходах и расходах организации, а также выявления конечного финансового результата деятельности организации за отчетный период.
Раздел IX - Забалансовые счета (001-011). Забалансовые счета в плане счетов предназначены для обобщения информации о наличии и движении ценностей, временно находящихся в пользовании или распоряжении организации (арендованных основных средств, материальных ценностей на ответственном хранении, в переработке и т.п.), условных прав и обязательств, а также для контроля за отдельными хозяйственными операциями
Введение
- Элементы электрических цепей.
- Топология электрических цепей.
- Переменный ток. Изображение синусоидальных переменных.
- Элементы цепи синусоидального тока, векторные диаграммы и комплексные соотношения для них.
- Основы символического метода расчета. Методы контурных токов и узловых потенциалов.
- Основы матричных методов расчета электрических цепей.
- Мощность в электрических цепях.
- Резонансные явления в цепях синусоидального тока.
- Векторные и топографические диаграммы. Преобразование линейных электрических цепей.
- Анализ цепей с индуктивно связанными элементами.
- Особенности составления матричных уравнений при наличии индуктивных связей и ветвей с идеальными источниками.
- Методы расчета, основанные на свойствах линейных цепей.
- Метод эквивалентного генератора. Теорема вариаций.
- Пассивные четырехполюсники.
- Электрические фильтры.
- Трехфазные электрические цепи: основные понятия и схемы соединения.
- Расчет трехфазных цепей.
- Применение векторных диаграмм для анализа несимметричных режимов. Мощность в трехфазных цепях.
- Метод симметричных составляющих.
- Теорема об активном двухполюснике для симметричныхсоставляющих.
- Вращающееся магнитное поле. Принцип действия асинхронного и синхронного двигателей.
- Линейные электрические цепи при несинусоидальных периодических токах.
- Резонансные явления в цепях несинусоидального тока. Высшие гармоники в трехфазных цепях.
- Переходные процессы в линейных электрических цепях. Классический метод расчета переходных процессов.
- Методика и примеры расчета переходных процессов классическим методом.
- Определение постоянной времени. Переходные процессы в R-L-C-цепи.
- Операторный метод расчета переходных процессов.
- Последовательность расчета переходных процессов операторным методом. Формулы включения. Переходные проводимость и функция по напряжению.
- Интеграл Дюамеля. Метод переменных состояния.
- Нелинейные цепи постоянного тока. Графические методы расчета.
- Расчет нелинейных цепей методом эквивалентного генератора. Аналитические и итерационные методы расчета цепей постоянного тока.
- Нелинейные магнитные цепи при постоянных потоках.
- Общая характеристика задач и методов расчета магнитных цепей.
- Особенности нелинейных цепей переменного тока. Графический метод расчета с использованием характеристик для мгновенных значений.
- Графические методы расчета с использованием характеристик по первым гармоникам и действующим значениям. Феррорезонанс. Аналитические методы расчета.
- Метод кусочно-линейной аппроксимации. Метод гармонического баланса.
- Понятие об эквивалентном эллипсе, заменяющем петлю гистерезиса. Потери в стали. Катушка и трансформатор с ферромагнитными сердечниками.
- Переходные процессы в нелинейных цепях. Аналитические методы расчета.
- Понятие о графических методах анализа переходных процессов в нелинейных цепях. Методы переменных состояния и дискретных моделей.
- Цепи с распределенными параметрами в стационарных режимах: основные понятия и определения.
- Линия без искажений. Уравнения линии конечной длины. Определение параметров длинной линии. Линия без потерь. Стоячие волны.
- Входное сопротивление длинной линии. Переходные процессы в цепях с распределенными параметрами.
- Сведение расчета переходных процессов в цепях с распределенными параметрами к нулевым начальным условиям. Правило удвоения волны.
| Теория / ТОЭ / Лекция N 1. Элементы электрических цепей. |
Электромагнитные процессы, протекающие в электротехнических устройствах, как правило, достаточно сложны. Однако во многих случаях, их основные характеристики можно описать с помощью таких интегральных понятий, как: напряжение, ток, электродвижущая сила (ЭДС). При таком подходе совокупность электротехнических устройств, состоящую из соответствующим образом соединенных источников и приемников электрической энергии, предназначенных для генерации, передачи, распределения и преобразования электрической энергии и (или) информации, рассматривают как электрическую цепь. Электрическая цепь состоит из отдельных частей (объектов), выполняющих определенные функции и называемых элементами цепи. Основными элементами цепи являются источники и приемники электрической энергии (сигналов). Электротехнические устройства, производящие электрическую энергию, называются генераторами или источниками электрической энергии, а устройства, потребляющие ее – приемниками (потребителями) электрической энергии.
У каждого элемента цепи можно выделить определенное число зажимов (полюсов), с помощью которых он соединяется с другими элементами. Различают двух –и многополюсные элементы. Двухполюсники имеют два зажима. К ним относятся источники энергии (за исключением управляемых и многофазных), резисторы, катушки индуктивности, конденсаторы. Многополюсные элементы – это, например, триоды, трансформаторы, усилители и т.д.
Все элементы электрической цепи условно можно разделить на активные и пассивные. Активным называется элемент, содержащий в своей структуре источник электрической энергии. К пассивным относятся элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности и конденсаторы) энергия. К основным характеристикам элементов цепи относятся их вольт-амперные, вебер-амперные и кулон-вольтные характеристики, описываемые дифференциальными или (и) алгебраическими уравнениями. Если элементы описываются линейными дифференциальными или алгебраическими уравнениями, то они называются линейными, в противном случае они относятся к классу нелинейных. Строго говоря, все элементы являются нелинейными. Возможность рассмотрения их как линейных, что существенно упрощает математическое описание и анализ процессов, определяется границами изменения характеризующих их переменных и их частот. Коэффициенты, связывающие переменные, их производные и интегралы в этих уравнениях, называются параметрами элемента.
Если параметры элемента не являются функциями пространственных координат, определяющих его геометрические размеры, то он называетсяэлементом с сосредоточенными параметрами. Если элемент описывается уравнениями, в которые входят пространственные переменные, то он относится к классу элементов с распределенными параметрами. Классическим примером последних является линия передачи электроэнергии (длинная линия).
Цепи, содержащие только линейные элементы, называются линейными. Наличие в схеме хотя бы одного нелинейного элемента относит ее к классу нелинейных.
Рассмотрим пассивные элементы цепи, их основные характеристики и параметры.
1. Резистивный элемент (резистор)
Условное графическое изображение резистора приведено на рис. 1,а. Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. Последнее определяется геометрическими размерами тела и свойствами материала: удельным сопротивлением r (Ом´ м) или обратной величиной – удельной проводимостью  (См/м).
В простейшем случае проводника длиной (См/м).
В простейшем случае проводника длиной 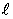 и сечением S его сопротивление определяется выражением и сечением S его сопротивление определяется выражением
 . .
 В общем случае определение сопротивления связано с расчетом поля в проводящей среде, разделяющей два электрода.
Основной характеристикой резистивного элемента является зависимость В общем случае определение сопротивления связано с расчетом поля в проводящей среде, разделяющей два электрода.
Основной характеристикой резистивного элемента является зависимость 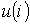 (или (или  ), называемая вольт-амперной характеристикой (ВАХ). Если зависимость ), называемая вольт-амперной характеристикой (ВАХ). Если зависимость 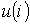 представляет собой прямую линию, проходящую через начало координат (см.рис. 1,б), то резистор называется линейным и описывается соотношением представляет собой прямую линию, проходящую через начало координат (см.рис. 1,б), то резистор называется линейным и описывается соотношением
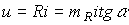 или
или
 ,
где ,
где 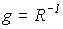 - проводимость. При этом R=const.
Нелинейный резистивный элемент, ВАХ которого нелинейна (рис. 1,б), как будет показано в блоке лекций, посвященных нелинейным цепям, характеризуется несколькими параметрами. В частности безынерционному резистору ставятся в соответствие статическое - проводимость. При этом R=const.
Нелинейный резистивный элемент, ВАХ которого нелинейна (рис. 1,б), как будет показано в блоке лекций, посвященных нелинейным цепям, характеризуется несколькими параметрами. В частности безынерционному резистору ставятся в соответствие статическое  и дифференциальное и дифференциальное  сопротивления.
2. Индуктивный элемент (катушка индуктивности)
Условное графическое изображение катушки индуктивности приведено на рис. 2,а. Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле. сопротивления.
2. Индуктивный элемент (катушка индуктивности)
Условное графическое изображение катушки индуктивности приведено на рис. 2,а. Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле.
 Индуктивность определяется отношением потокосцепления к току, протекающему по виткам катушки,
Индуктивность определяется отношением потокосцепления к току, протекающему по виткам катушки,
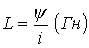 .
В свою очередь потокосцепление равно сумме произведений потока, пронизывающего витки, на число этих витков .
В свою очередь потокосцепление равно сумме произведений потока, пронизывающего витки, на число этих витков 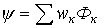 , где , где  .
Основной характеристикой катушки индуктивности является зависимость .
Основной характеристикой катушки индуктивности является зависимость 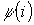 , называемая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость , называемая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость 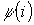 представляет собой прямую линию, проходящую через начало координат (см. рис. 2,б); при этом представляет собой прямую линию, проходящую через начало координат (см. рис. 2,б); при этом
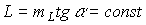 .
Нелинейные свойства катушки индуктивности (см. кривую .
Нелинейные свойства катушки индуктивности (см. кривую 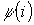 на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала, для которого зависимость на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала, для которого зависимость  магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного гистерезиса нелинейная катушка характеризуется статической магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного гистерезиса нелинейная катушка характеризуется статической  и дифференциальной и дифференциальной 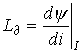 индуктивностями.
3. Емкостный элемент (конденсатор)
Условное графическое изображение конденсатора приведено на рис. 3,а. индуктивностями.
3. Емкостный элемент (конденсатор)
Условное графическое изображение конденсатора приведено на рис. 3,а.
 Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета последней необходимо рассчитать электрическое поле в конденсаторе. Емкость определяется отношением заряда q на обкладках конденсатора к напряжению u между ними
Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета последней необходимо рассчитать электрическое поле в конденсаторе. Емкость определяется отношением заряда q на обкладках конденсатора к напряжению u между ними
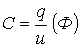 и зависит от геометрии обкладок и свойств диэлектрика, находящегося между ними. Большинство диэлектриков, используемых на практике, линейны, т.е. у них относительная диэлектрическая проницаемость
и зависит от геометрии обкладок и свойств диэлектрика, находящегося между ними. Большинство диэлектриков, используемых на практике, линейны, т.е. у них относительная диэлектрическая проницаемость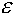 =const. В этом случае зависимость =const. В этом случае зависимость 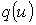 представляет собой прямую линию, проходящую через начало координат, (см. рис. 3,б) и представляет собой прямую линию, проходящую через начало координат, (см. рис. 3,б) и
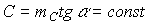 .
У нелинейных диэлектриков (сегнетоэлектриков) диэлектрическая проницаемость является функцией напряженности поля, что обусловливает нелинейность зависимости .
У нелинейных диэлектриков (сегнетоэлектриков) диэлектрическая проницаемость является функцией напряженности поля, что обусловливает нелинейность зависимости 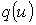 (рис. 3,б). В этом случае без учета явления электрического гистерезиса нелинейный конденсатор характеризуется статической (рис. 3,б). В этом случае без учета явления электрического гистерезиса нелинейный конденсатор характеризуется статической 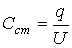 и дифференциальной и дифференциальной  емкостями.
Схемы замещения источников электрической энергии
Свойства источника электрической энергии описываются ВАХ емкостями.
Схемы замещения источников электрической энергии
Свойства источника электрической энергии описываются ВАХ 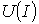 , называемой внешней характеристикой источника. Далее в этом разделе для упрощения анализа и математического описания будут рассматриваться источники постоянного напряжения (тока). Однако все полученные при этом закономерности, понятия и эквивалентные схемы в полной мере распространяются на источники переменного тока. ВАХ источника может быть определена экспериментально на основе схемы, представленной на рис. 4,а. Здесь вольтметр V измеряет напряжение на зажимах 1-2 источника И, а амперметр А – потребляемый от него ток I, величина которого может изменяться с помощью переменного нагрузочного резистора (реостата) RН. , называемой внешней характеристикой источника. Далее в этом разделе для упрощения анализа и математического описания будут рассматриваться источники постоянного напряжения (тока). Однако все полученные при этом закономерности, понятия и эквивалентные схемы в полной мере распространяются на источники переменного тока. ВАХ источника может быть определена экспериментально на основе схемы, представленной на рис. 4,а. Здесь вольтметр V измеряет напряжение на зажимах 1-2 источника И, а амперметр А – потребляемый от него ток I, величина которого может изменяться с помощью переменного нагрузочного резистора (реостата) RН.
 В общем случае ВАХ источника является нелинейной (кривая 1 на рис. 4,б). Она имеет две характерные точки, которые соответствуют:
а – режиму холостого хода
В общем случае ВАХ источника является нелинейной (кривая 1 на рис. 4,б). Она имеет две характерные точки, которые соответствуют:
а – режиму холостого хода  ;
б –режиму короткого замыкания ;
б –режиму короткого замыкания 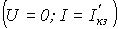 .
Для большинства источников режим короткого замыкания (иногда холостого хода) является недопустимым. Токи и напряжения источника обычно могут изменяться в определенных пределах, ограниченных сверху значениями, соответствующими номинальному режиму (режиму, при котором изготовитель гарантирует наилучшие условия его эксплуатации в отношении экономичности и долговечности срока службы). Это позволяет в ряде случаев для упрощения расчетов аппроксимировать нелинейную ВАХ на рабочем участке m-n (см. рис. 4,б) прямой, положение которой определяется рабочими интервалами изменения напряжения и тока. Следует отметить, что многие источники (гальванические элементы, аккумуляторы) имеют линейные ВАХ.
Прямая 2 на рис. 4,б описывается линейным уравнением .
Для большинства источников режим короткого замыкания (иногда холостого хода) является недопустимым. Токи и напряжения источника обычно могут изменяться в определенных пределах, ограниченных сверху значениями, соответствующими номинальному режиму (режиму, при котором изготовитель гарантирует наилучшие условия его эксплуатации в отношении экономичности и долговечности срока службы). Это позволяет в ряде случаев для упрощения расчетов аппроксимировать нелинейную ВАХ на рабочем участке m-n (см. рис. 4,б) прямой, положение которой определяется рабочими интервалами изменения напряжения и тока. Следует отметить, что многие источники (гальванические элементы, аккумуляторы) имеют линейные ВАХ.
Прямая 2 на рис. 4,б описывается линейным уравнением
где Уравнение (1) позволяет составить последовательную схему замещения источника (см. рис. 5,а). На этой схеме символом Е обозначен элемент, называемый идеальным источником ЭДС. Напряжение на зажимах этого элемента
Если ВАХ источника линейна, то для определения параметров его схемы замещения необходимо провести замеры напряжения и тока для двух любых режимов его работы. Существует также параллельная схема замещения источника. Для ее описания разделим левую и правую части соотношения (1) на
или
где Уравнению (2) соответствует схема замещения источника на рис. 6,а.
На этой схеме символом J обозначен элемент, называемый идеальным источником тока. Ток в ветви с этим элементом равен Отметим, что в расчетном плане при выполнении условия Кроме отмеченных режимов функционирования источника, на практике важное значение имеет согласованный режим работы, при котором нагрузкой RН от источника потребляется максимальная мощность
Условие такого режима
В заключение отметим, что в соответствии с ВАХ на рис. 5,б и 6,б идеальные источники ЭДС и тока являются источниками бесконечно большой мощности. Литература
Контрольные вопросы и задачи
Ответ: L=0,1 Гн; WМ=40 Дж.
Ответ: С=0,5 мкФ; WЭ=0,04 Дж.
Ответ:
Ответ: |
| Теория / ТОЭ / Лекция N 2. Топология электрической цепи. |
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.

Ветвью называется участок цепи, обтекаемый одним и тем же током. Узел – место соединения трех и более ветвей. Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.
Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом. Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным. Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе. В теории электрических цепей важное значение имеют следующие подграфы: 1. Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно. 2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. Если между любой парой узлов графа существует связь, то граф называют связным. 3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.
Рис.4 4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа. Если граф содержит m узлов и n ветвей, то число ветвей любого дерева 5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом. Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S1 и S2. При этом получаем соответственно сечения, образованные ветвями 6-4-5 и 6-2-1-5. С понятием дерева связаны понятия главных контуров и сечений:
|
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1006; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 ,
,
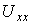 - напряжение на зажимах источника при отключенной нагрузке (разомкнутом ключе К в схеме на рис. 4,а);
- напряжение на зажимах источника при отключенной нагрузке (разомкнутом ключе К в схеме на рис. 4,а); 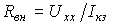 - внутреннее сопротивление источника.
- внутреннее сопротивление источника.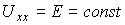 не зависит от тока источника, следовательно, ему соответствует ВАХ на рис. 5,б. На основании (1) у такого источника
не зависит от тока источника, следовательно, ему соответствует ВАХ на рис. 5,б. На основании (1) у такого источника 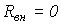 . Отметим, что направления ЭДС и напряжения на зажимах источника противоположны.
. Отметим, что направления ЭДС и напряжения на зажимах источника противоположны.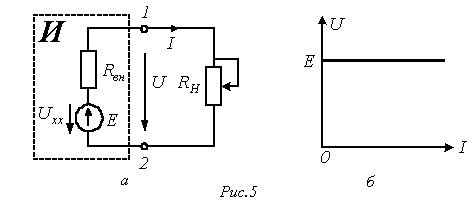
 . В результате получим
. В результате получим
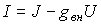 ,
,
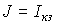 ;
;  - внутренняя проводимость источника.
- внутренняя проводимость источника.
 , т.е. его внутреннее сопротивление
, т.е. его внутреннее сопротивление 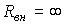 .
. последовательная и параллельная схемы замещения источника являются эквивалентными. Однако в энергетическом отношении они различны, поскольку в режиме холостого хода для последовательной схемы замещения мощность равна нулю, а для параллельной – нет.
последовательная и параллельная схемы замещения источника являются эквивалентными. Однако в энергетическом отношении они различны, поскольку в режиме холостого хода для последовательной схемы замещения мощность равна нулю, а для параллельной – нет. ,
,
 ,
,


 Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.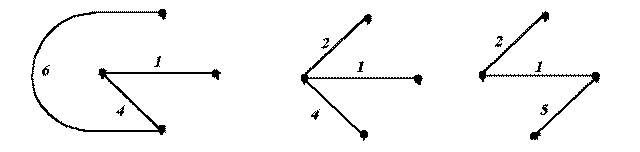
 , а числа ветвей связи графа
, а числа ветвей связи графа  .
.