
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства кратных интегралов
|
|
|
|
1°. Линейность: Множество RM функций интегрируемых на множестве М – линейное
пространство, а 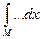 – линейный функционал.
– линейный функционал.
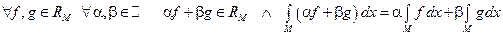 .
.
2°. Условие нормировки: 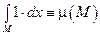 . Другая форма записи
. Другая форма записи 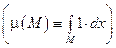 по сути дела определяет меру произвольного множества из евклидового пространства.
по сути дела определяет меру произвольного множества из евклидового пространства.
3°. Если интеграл по множеству Лебеговой меры ноль существует, то он
равен нулю.
Примечание: Множество М называется множеством Лебеговой меры ноль,
если 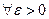
 такие, что
такие, что 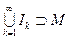 и
и 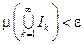 .
.
4°. а. 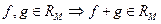 ; б.
; б. 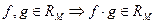 ;
;
в. если  и
и 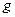 – отделена от нуля на М, то
– отделена от нуля на М, то 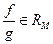
5°.  и f = g п.в. (почти всюду) на М, то
и f = g п.в. (почти всюду) на М, то 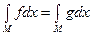 .
.
6°. Аддитивность: Если 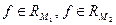 и
и 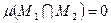 то
то
 ,
,
В общем случае:  .
.
Δ. Следует из равенства: 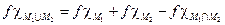 ▲
▲
7°. Монотонность: 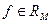 и
и 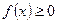 то
то  .
.
8°. Интегрирование неравенств: если 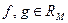 и
и 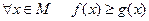 то
то
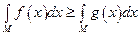 .
.
9°. Пусть 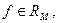
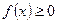
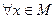 . Для того чтобы
. Для того чтобы  , необходимо и достаточно чтобы существовала внутренняя точка множества М, в которой f (x) > 0 и непрерывна.
, необходимо и достаточно чтобы существовала внутренняя точка множества М, в которой f (x) > 0 и непрерывна.
10°. Интегрируемость модуля интегрируемой функции:  .
.
11°. Теорема о среднем:  ,
, 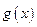 на М сохраняет знак и
на М сохраняет знак и 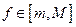 , то
, то

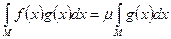 .
.
Если множество М – связно и f (x) – непрерывна на 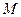 то
то 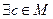 такое, что
такое, что 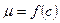 .
.
12°. Для того чтобы интеграл от неотрицательной функции был равен 0
необходимо и достаточно, чтобы f (x) = 0 почти всюду на М.
13°. Теорема Фубини. Для двойного интеграла:
Пусть область 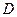 – прямоугольник:
– прямоугольник:  . Тогда, при условии существования внутренних однократных интегралов, для нахождения двойного интеграла можно перейти к повторному интегрированию (см. рис. а):
. Тогда, при условии существования внутренних однократных интегралов, для нахождения двойного интеграла можно перейти к повторному интегрированию (см. рис. а):

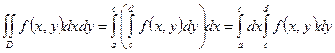 , или
, или
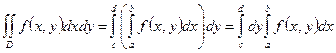 .
.
 Если область интегрирования не прямоугольник, теорема Фубини все равно справедлива и имеет вид (см. рис. б):
Если область интегрирования не прямоугольник, теорема Фубини все равно справедлива и имеет вид (см. рис. б): 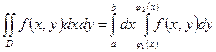 . (*)
. (*)
Примечание: Внешние пределы интегрирования должны быть константами, внутренние пределы интегрирования могут зависеть от переменной, по которой интегрирование ещё предстоит.
Формула (*) может быть получена с использованием характеристической функции множества D.
Для многократного интеграла:
Пусть 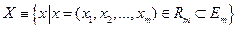 и
и 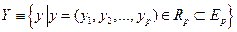 некоторые подмножества евклидовых пространств
некоторые подмножества евклидовых пространств 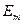 и
и  . Определим декартово произведение этих множеств, являющееся подмножеством евклидового пространства
. Определим декартово произведение этих множеств, являющееся подмножеством евклидового пространства  :
: 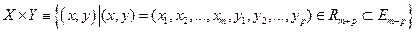 .
.
Тогда теорема Фубини для  имеет вид:
имеет вид: 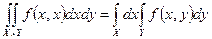 .
.
Теорема справедлива и для брусов X и Y, и для более сложных конфигураций.
Примеры:
10. Вычислить  , если граница области
, если граница области 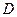 задана уравнениями:
задана уравнениями:
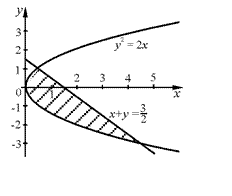
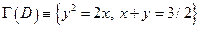
 . Находя точки пересечения кривых определяющих границу области, получаем две точки:
. Находя точки пересечения кривых определяющих границу области, получаем две точки: 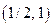 и
и  . Тогда возможная расстановка пределов интегрирования при переходе к повторным интегралам дает:
. Тогда возможная расстановка пределов интегрирования при переходе к повторным интегралам дает:
а). 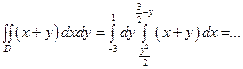 ;
;
б). 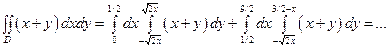 .
.
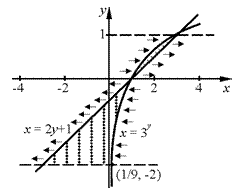 20. Изменить порядок интегрирования в повторном интеграле:
20. Изменить порядок интегрирования в повторном интеграле:  .
.
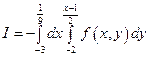 –
–
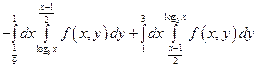 .
.
Рецепт: При расстановке пределов интегрирования в двойном интеграле рекомендуется начинать с внешних пределов интегрирования.
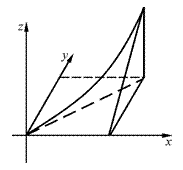 30. Вычислить:
30. Вычислить: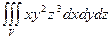 , если
, если 
Переход к повторным интегралам даёт: 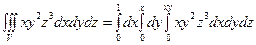 .
.
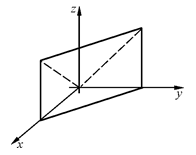
При этом, в тройном интеграле расстановку пределов надо начинать с внутренних пределов интегрирования. Затем спроецировать область V на плоскость xOy
расставив пределы в области D – лежащей в плоскости xOy.
40. Изменить порядок интегрирования в повторном интеграле: 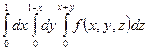 .
.
а).  ;
;
б).  .
.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1799; Нарушение авторских прав?; Мы поможем в написании вашей работы!