Криволинейные и поверхностные интегралы

ДОПОЛНЕНИЕ 2

В поверхностном интеграле второго рода часто обозначают:

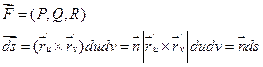где .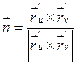

Общая формула Стокса −формула Ньютона-Лейбница-Грина-Остроградского-Гаусса-Стокса-Пуанкаре

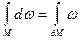
где 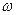-дифференциальная ()-форма, -внешний дифференциал формы, 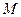-многообразие (можно цепь) размерности 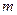с краем –многообразием(соответственно цепью) размерности .

Формула Ньютона-Лейбница: криволинейный интеграл второго рода вдоль кусочно-гладкой ориентированной кривой с началом в точке 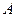и концом в точке 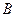от градиента числового поля,непрерывно дифференцируемого на этой кривой, равен разности значений поля в конечной и в начальной точках

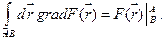
Функция называется непрерывно дифференцируемой на кривой 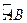,если она непрерывно дифференцируема в некоторой окрестности носителя этой кривой.

То же самое, записанное в координатной форме, криволинейный интеграл второго рода вдоль кусочно-гладкой ориентированной кривой с началом в точке 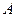и концом в точке 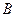от дифференциала непрерывно дифференцируемой на этой кривой функции, равен разности её значений в конечной и начальной точках:

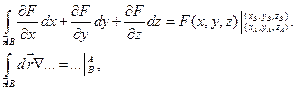
где вместо многоточия можно подставить тензорнозначную ф-ю непрерывно дифференцируемую на кривой 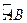, т.е. в некоторой окрестности этой кривой.

Геометрическое определение градиента: проекция на фиксированный орт 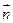градиента в точке скалярной ф-и ,непрерывно дифференцируемой в некоторой окрестности точки ,равная пределу отношения разности значения этой ф-ии на концах произвольного отрезка прямой, проходящего вдоль направления орта 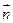через точку и содержащегося в указанной окрестности, к длине этого отрезка 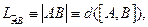когда диаметр отрезка стремится к нулю

Формула Остроградского-Гаусса: интеграл по объёму,ограниченному замкнутой кусочно-гладкой ориентируемой поверхностью, от дивергенции векторного поля, непрерывно дифференцируемого на замыкании этого объёма, т.е. на объеме вместе с краем, равен потоку поля через поверхность, ограничивающую объём, и ориентированную внешней нормалью

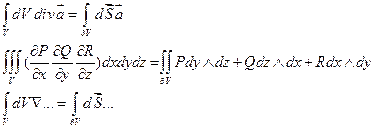
Геометрическое определение дивергенции

Формула Стокса: поток ротора векторного поля через кусочно-гладкую ориентированную поверхность с кусочно-гладким краем,ориентированным так, что с конца ориентирующего вектора нормали к поверхности обход края в положительном направлении выглядит происходящим против часовой стрелки,равен циркуляции этого вектора по краю поверхности

предполагается, что компоненты поля и их производные,встречающиеся в роторе, непрерывны на поверхности 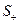вместе с краем 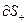, т.е. в некоторой окрестности этого множества .

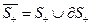В координатной записи формулы Стокса,для сокращения записи, знак внешнего умножения часто подразумевают, но не пишут.

Дата добавления: 2014-01-11