Вычисление определителя по методу Гаусса

Вычисление определителя. Общие положения

Одной из важных задач линейной алгебры является вычисление значения определителя квадратной матрицы. Можно привести, в частности, некоторые задачи, сопровождаемые вычислением определителей:

1) численные решение системы имеет смысл только в том случае, если определитель отличен от нуля;

2) если определитель мал по абсолютной величине, то вычисленные корни могут значительно отличаться от истинных;

3) при получении множественного коэффициента корреляции и частных коэффициентов корреляции необходимо неоднократно выполнять вычисление различных определителей, т.е. в этом случае вычисление определителей представляет и самостоятельный интерес.

Поэтому оказывается полезным сопровождение решения системы линейных уравнений вычислением определителя.

Существуют различные методы вычисления определителя. Рассмотрим один из них, а именно основанный на изложенный выше метод Гаусса.

Обозначим определитель системы (4.1) через D. При приведении матрицы системы (4.1) к треугольному виду необходимо правую и левую части первого уравнения разделить на ведущий элемент 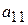. В этом случае определитель преобразованной системы будет . Последующие преобразования, связанные с исключением 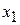из остальных уравнений системы, величину определителя не изменяют.

На втором шаге, когда необходимо разделить обе части (преобразованного) второго уравнения на второй преобразованный элемент 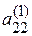, определитель полученной системы будет . Операции по исключению из уравнений системы вновь не изменяют величину определителя.

На n- м шаге, осуществляя аналогичные действия, приходим к системе (4.1), определитель которой, очевидно, будет равен 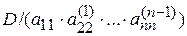. Но матрица коэффициентов при неизвестных преобразованной системы – треугольная, с единицами по главной диагонали, поэтому ее определитель равен 1: 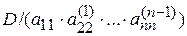= 1, следовательно,

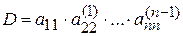(5.1)

Таким образом, значение определителя системы (4.1) получается как произведение ведущих элементов, используемых на каждом шаге.

Дата добавления: 2014-01-11