Назначение Mathcad

Задача о доставке

Задача коммивояжера

Коммивояжеру, находящемуся в Париже, необходимо посетить три города. Он получил информацию о стоимости проезда самолетом в каждый из выбранных городов и стоимость проезда из одного города в другой. На основе добытых данных он составил матрицу стоимостей (см. табл.) проезда в выбранные города и обратно. Зная матрицу стоимостей коммивояжеру надо так составить маршрут путешествия, чтобы затраты на путешествие были бы минимальными и чтобы выполнялось требование: каждый пункт посещается только один раз.

Пункты	Париж	Берлин	Рим	Лондон
Париж
Берлин
Рим
Лондон

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

0x₁₁+270× x₁₂+430× x₁₃+160× x₁₄+70× x₂₁+0× x₂₂+160x₂₃+10x₂₄+200× x₃₁+130x₃₂+0× x₃₃+ +350× x₃₄+210× x₄₁+160x₄₂+250× x₄₃+0× x_44® min,

Ограничения имеют вид:

x₁₁+x₂₁+x₃₁+x₄₁=1,

x₁₂+x₂₂+x₃₂+x₄₂=1,

x₁₃+x₂₃+x₃₃+x₄₃=1.

x₁₄+x₂₄+x₃₄+x₄₄=1,

x₁₁+x₁₂+x₁₃+x₁₄=1,

x₂₁+x₂₂+x₂₃+x₂₄=1,

x₃₁+x₃₂+x₃₃+x₃₄=1,

x₄₁+x₄₂+x₄₃+x₄₄=1,

u₂-u₃+3× x_23£ 2,

u₂-u₄+3× x_24£ 2,

u₃-u₂+3× x_32£ 2,

u₃-u₄+3× x_34£ 2,

u₄-u₂+3× x_42£ 2,

u₄-u₃+3× x_43£ 2.

Вид электронной таблицы, созданной для решения задачи, представлен на рис. 40. Значения переменных x_ij располагаются в блоке B3:E6. В данном блоке ячейки, расположенные по диагонали обнулены (пункт назначения не может быть одновременно пунктом прибытия) и выделены, для удобства задания ограничений. Даны стоимости проезда из города в город (блок B11:E14). Для вычислений необходимо задать размерность задачи n (количество городов)- ячейка F16.

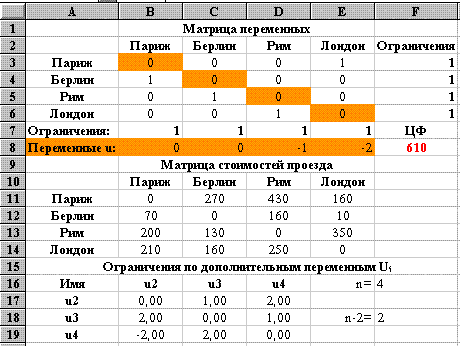
Рис. 40

Целевая функция расположена в ячейке F8. Ограничения находятся в блоках B7:E7 (коммивояжер въезжает один раз в каждый город) и F3:F6 (коммивояжер выезжает из каждого города один раз) (см. рис. 40 и 41). Вид электронной таблицы в режиме отображения формул представлен на рис. 41. В задаче коммивояжера есть ряд специфических ограничений по дополнительным переменным u_i (см. мат модель). Формулы этих ограничений находятся в блоке ячеек B17:E19. Значения самих переменных располагаются в блоке B8:E8.

На рис. 42 представлена запись условий задачи в окне "Поиск решения". Как известно, дополнительные переменные не относятся к целевой функции, но они, также как и x_ij, являются изменяемыми, поэтому адреса содержащих их ячеек должны быть введены в поле Изменяя ячейки одновременно с адресами переменных целевой функции.

Операцию ввода удобно проводить с помощью мыши. Необходимо установить курсор ввода в поле Изменяя ячейки, затем выделить мышью блок ячеек переменных целевой функции, нажать <Ctrl> и, удерживая эту клавишу, выделить мышью блок ячеек рабочего листа, отведенный для переменных u_i. В поле ввода адреса блоков отделяются ";" (см. рис. 42).

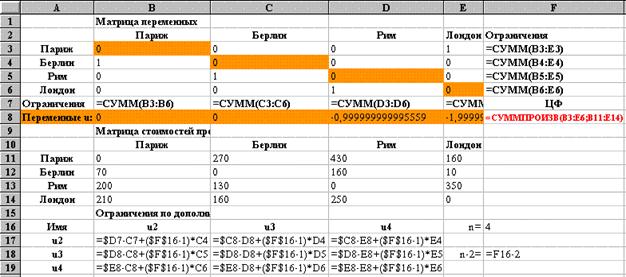
Рис. 41

Перечислим ограничения, которых не видно на рис. 42: $C$4=0; $D$5=0; $E$6=0; $F$3:$F$6=1.

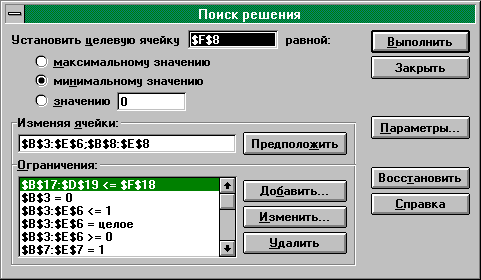
Рис. 42

Первая запись в группе Ограничения представляет собой совокупность ограничений по дополнительным переменным u_i. Каждая ячейка блока в левой части неравенства содержит формулу одного ограничения (см. рис. 41 и мат. модель), правую часть представляет одно значение, равное n-2, содержащееся в F18. Такая запись означает, что каждая ячейка блока $B$17:$D$19 меньше либо равна 2 (4-2=2).

В поиске решения нельзя явно задать ограничение i¹ j. Исходя из смысла переменных x_ij можно предположить, что значения тех x_ij, для которых i=j (расположенных по диагонали в блоке переменных), всегда должны быть равны 0 и ввести соответствующие ограничения. В группе Ограничения таких ограничений четыре: $B$3=0, $C$4=0, $D$5=0, $E$6=0.

По результатам поиска решения найден ответ задачи: из Парижа коммивояжер летит в Лондон, оттуда в Рим, затем в Берлин, откуда возвращается в Париж. Общая стоимость перелета составит 610 д. е. (см. рис. 40).

Фирма обслуживает 5 клиентов. Каждый день она доставляет своим клиентам товары на грузовых машинах. Существует 3 допустимых маршрута доставки, каждый из которых позволяет обслужить определенное количество клиентов и требует использования в течении дня одного транспортного средства. Каждый маршрут характеризуется определенными расходами (см. табл.). Необходимо выбрать такое множество маршрутов, при котором обеспечивается обслуживание каждого из клиентов и, кроме того, суммарные расходы минимальны, при условии, что каждый клиент обслуживается один раз в день.

Таблица обслуживания клиентов по маршрутам
Клиенты	Маршруты
Расходы по маршруту

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

900× x₁+1000× x₂+800× x_3® min,

Ограничения имеют вид:

1× x₁₁+0× x₂₁+1× x₃₁=1,

1× x₁₂+0× x₂₂+0× x₃₂=1,

1× x₁₃+0× x₂₃+1× x₃₃=1,

0× x₁₂+1× x₂₂+0× x₃₂=1,

0× x₁₃+1× x₂₃+1× x₃₃=1.

Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. 43. Значения переменных x_j располагаются в блоке ячеек B10:D10 (см. рис. 43). Коэффициенты целевой функции, отражающие стоимость доставки по маршруту, находятся по адресам B9:D9. Данные об обслуживании клиентов по маршрутам имеются в блоке B4:D8

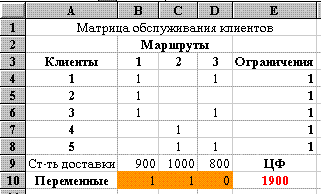
Рис. 43

Формулы целевой функции и ограничений находятся соответственно в ячейке E10 и ячейках E4:E8 (каждый клиент обслуживается по каждому маршруту только один раз в день) (см. рис. 43 и 44). Вид электронной таблицы в режиме отображения формул представлен на рис. 44.

Рис. 44

Запись условий задачи в окне "Поиск решения" можно увидеть на рис. 45.

Результаты поиска решения приведены на рис. 43.

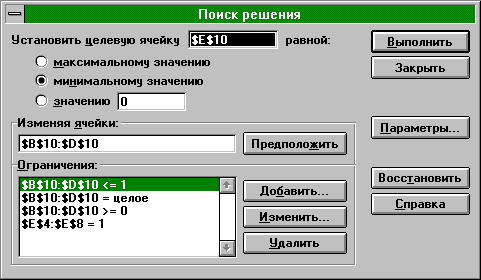
Рис. 45

Лекция №5

Тема: Работа в Mathcad

Mathcad является математическим редактором, позволяющим проводить разнообразные научные и инженерные расчеты, начиная от элементарной арифметики и заканчивая сложными реализациями численных методов. С точки зрения классификации программного обеспечения, пакет Mathcad — типичный представитель класса PSE-приложений. Пользователи Mathcad — это студенты, ученые, инженеры, разнообразные технические специалисты и все, кому приходится проводить математические расчеты. Благодаря простоте применения, наглядности математических действий, обширной библиотеке встроенных функций и численных методов, возможности символьных вычислений, а также превосходному аппарату представления результатов (графики самых разных типов, мощных средств подготовки печатных документов и Web-страниц) Mathcad стал наиболее популярным математическим приложением.

Что из себя представляет система Mathcad? Следует хорошо представлять себе, что в состав Mathcad входят несколько интегрированных между собой компонентов:

мощный текстовый редактор, позволяющий вводить, редактировать и форматировать как текст, так и математические выражения;

вычислительный процессор, умеющий проводить расчеты по введенным формулам, используя встроенные численные методы;

символьный процессор, позволяющий проводить аналитические вычисления и являющийся, фактически, системой искусственного интеллекта;

огромное хранилище справочной информации, как математической, так и инженерной, оформленной в качестве интерактивной электронной книги.

Отличительной чертой Mathcad от большинства других современных математических приложений является его построение по принципу WYSIWYG ("What You See Is What You Get" — "что вы видите, то и получите"). Поэтому он очень прост в использовании, в частности, из-за отсутствия необходимости сначала писать программу, реализующую те или иные математические расчеты, а потом запускать ее на исполнение. Вместо этого достаточно просто вводить математические выражения с помощью встроенного редактора формул, причем в виде, максимально приближенном к общепринятому, и тут же получать результат. Кроме того, можно изготовить на принтере печатную копию документа или создать страницу в Интернете именно в том виде, который этот документ имеет на экране компьютера при работе с Mathcad, либо можно включить документ в структуру электронной книги Mathcad.

Создатели Mathcad сделали все возможное, чтобы пользователь, не обладающий специальными знаниями в программировании (а таких большинство среди ученых и инженеров), мог в полной мере приобщиться к достижениям современной вычислительной науки и компьютерных технологий. Для эффективной работы с редактором Mathcad достаточно базовых навыков пользователя. С другой стороны, профессиональные программисты (к которым относит себя и автор этих строк) могут извлечь из Mathcad намного больше, создавая различные программные решения, существенно расширяющие возможности, непосредственно заложенные в Mathcad.

В соответствии с проблемами реальной жизни, математикам приходится решать одну или несколько из следующих задач:

ввод на компьютере разнообразных математических выражений (для дальнейших расчетов или создания документов, презентаций, Web-страниц или электронных книг);

проведение математических расчетов (как аналитических, так и при помощи численных методов);

подготовка графиков с результатами расчетов;

ввод исходных данных и вывод результатов в текстовые файлы или файлы с базами данных в других форматах;

подготовка отчетов работы в виде печатных документов;

подготовка Web-страниц и публикация результатов в Интернете;

получение различной справочной информации из области математики.

Со всеми этими (а также некоторыми другими) задачами с успехом справляется Mathcad:

математические выражения и текст вводятся с помощью формульного редактора Mathcad, который по возможностям и простоте использования не уступает, к примеру, редактору формул, встроенному в Microsoft Word;

математические расчеты производятся немедленно, в соответствии с введенными формулами;

графики различных типов (по выбору пользователя) с богатыми возможностями форматирования вставляются непосредственно в документы;

возможен ввод и вывод данных в файлы различных форматов;

документы могут быть распечатаны непосредственно в Mathcad в том виде, который пользователь видит на экране компьютера, или сохранены в формате RTF для последующего редактирования в более мощных текстовых редакторах (например, Microsoft Word);

возможно полноценное сохранение документов Mathcad в формате RTF-документов, а также Web-страниц: HTML и (начиная с 12-й версии) XML;

ПРИМЕЧАНИЕ

Начиная с 12-й версии, файлы Mathcad имеют формат ХМСО, являющийся разновидностью текстовой XML-разметки (и следующим шагом по сравнению с форматом MathML, примененным в 2001-й версии). Применение XML-формата оправдано, во-первых, тем, что он становится общеупотребительным для целого ряда приложений и данных самого различного типа. Во-вторых, удобство XML-файлов заключается в возможности использовать для просмотра и манипуляций с Mathcad-документами другие (предусматривающие это) приложения, например, для HTML-экспорта и т. п. Их можно также просматривать и редактировать "вручную", в любом текстовом редакторе.

имеется опция объединения разрабатываемых вами документов в электронные книги, которые, с одной стороны, позволяют в удобном виде хранить математическую информацию, а с другой — являются полноценными Mathcad-программами, способными осуществлять расчеты;

символьные вычисления позволяют осуществлять аналитические преобразования, а также мгновенно получать разнообразную справочную математическую информацию;

справочная система, а также многочисленные дополнительные материалы, оформленные в виде электронных книг (Ресурсы Mathcad), помогают быстро отыскать нужную математическую информацию или пример тех или иных расчетов.

Таким образом, следует хорошо представлять себе, что в состав Mathcad входит несколько интегрированных между собой компонентов — это мощный текстовый редактор для ввода и правки, как текста, так и формул, вычислительный процессор — для проведения расчетов согласно введенным формулам, и символьный процессор, являющийся, по сути, системой искусственного интеллекта. Сочетание этих компонентов создает удобную вычислительную среду для разнообразных математических расчетов и, одновременно, документирования результатов работы.

Дата добавления: 2014-01-11