Решение. В пункте 1) условия явно указано, что A, B и C являются исходными работами, поэтому изобразим их тремя стрелками

В пункте 1) условия явно указано, что A, B и C являются исходными работами, поэтому изобразим их тремя стрелками, выходящими из исходного события 1. Пункт 2) условия означает, что стрелки работ A и B должны окончиться в одном событии, из которого выйдет стрелка работы D. Но поскольку стрелки работ A и B также и начинаются в одном событии, то имеет место параллельность работ, которая недопустима правилами построения сетевых моделей (см. рис.5).

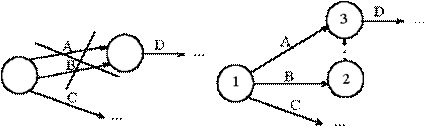
Рис.5. Устранение параллельности работ A и B

Для ее устранения введем дополнительное событие 2, в которое войдет работа B, после чего соединим события 2 и 3, в которые входят работы A и B пунктирной стрелкой фиктивной работы. В данном случае фиктивная работа (2,3) не соответствует никакой реальной работе, а лишь отображает логическую связь между работами B и D. Дальнейшее построение рассмотрим с помощью рис.6

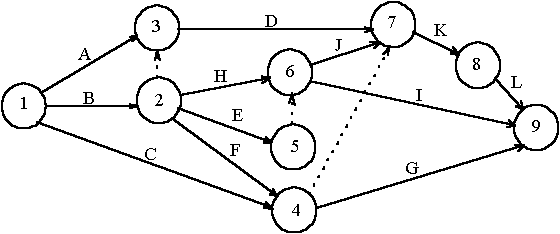
Рис.6. Сетевая модель задачи №2

Согласно пункту 3) условия задачи из события 2, выходят три стрелки работ E, F и H. Согласно пункту 4) условия задачи стрелки работ C и F должны войти в общее событие, из которого выйдет стрелка работы G. Проблема с параллельностью работ E и H [пункт 5) условия задачи] решается путем введения дополнительного события 5 и фиктивной работы (5,6). Для отображения в сетевой модели пункта 6) условия задачи введем стрелки работ D и J в событие 7, а связь работ F и C с работой K отобразим с помощью фиктивной работы (4,7). Стрелки работ F и C нельзя было напрямую вводить в событие 7, потому что после них должна следовать работа G, которая с работами D и J никак не связана. Стрелка работы L выходит из события 8, т.е. после окончания работы K в соответствии с пунктом 7) условия задачи.

Поскольку в условии не указано, что работы L, I и G предшествуют каким-либо другим работам, то эти работы являются завершающими и их стрелки войдут в завершающее событие 9. Нумерацию событий проводят после построения сетевого графика, следя за тем, чтобы номер начального события каждой работы был меньше номера ее конечного события

Задача.. В таблице 1 дан перечень работ, связанных с выпуском новой продукции.

Табл.1.

	Выполняемая работа	Продол-жительность tij	Предшест-вующие работы
А	Окончательный вариант		–
В	Технологический анализ		A
С	Подготовка схем		A
D	Выдача заявок на материалы		B
Е	Изготовление деталей		C, D
F	Выдача заявок на детали		B
G	Получение деталей		F
Н	Размещение субподрядов		B
I	Получение заказанных деталей		H
J	Сборка и испытания		E, G, I

Приводимый перечень работ показывает, что большинство работ обеспечивается поставками деталей с собственных складов, по субподрядам и за счет их производства на самом предприятии. Необходимо:

1. Построить сетевой график выпуска.

2. Определить ранние(t_р[i]) и поздние(t_п[i]) сроки свершения событий найти критический путь.

3. Построить линейный график.

Решение.

1. На основании перечня работ и условий предшествования строим сетевой график, показанный на рис.1. События сетевого графика пронумерованы в соответствии с алгоритмом, приведенным в [2].

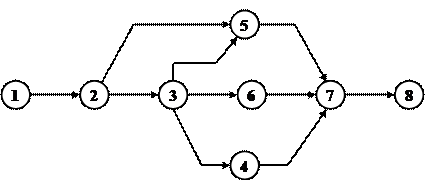Рис.1. Сетевой график к примеру 1.

2. Вычислительный процесс, используемый для определения ранних сроков свершения событий сетевого графика, называется прямым проходом. При прямом проходе вычисления начинаются с исходного события и продолжаются последовательно слева направо в порядке возрастания номеров событий до тех пор, пока не будут определены ранние сроки свершения событий для каждого события сетевого графика.

Для исходного события ранний срок свершения полагается равным нулю. Ранний срок свершения для последующего события определяется простым прибавлением длительности последующей работы к раннему моменту предшествующего события.

Если в событие входит несколько работ, то его ранним сроком свершения события считается наибольшее из всех ранних времен окончания этих работ.

В данном примере:

t_р[1] = 0;

t_р[2] = t_р[1] + t₁₂ = 0 + 4 = 4;

t_р[3] = t_р[2] + t₂₃ = 4 + 2 = 6;

t_р[4] = t_р[3] + t₃₄ = 6 + 3 = 9;

t_р[5] = max(t_р[2] + t₂₅, t_р[3] + t₃₅) = max(4 + 3, 6 + 2) = 8;

t_р[6] = t_р[3] + t₃₆ = 6 + 1 = 7;

t_р[7] = max(t_р[4] + t₄₇, t_р[5] + t₅₇, t_р[6] + t₆₇) =

= max(9 + 4, 8 + 1, 7 + 3) = 13;

t_р[8] = t_р[7] + t₇₈ = 13 + 2 = 15;

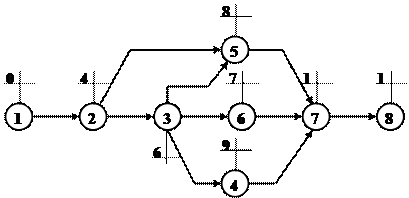Вычислительный процесс для определения поздних сроков свершения событий называется обратным проходом.

Рис.2. Ранние сроки свершения событий

Найденные значения ранних сроков свершения событий показаны на рис.2.

При обратном проходе вычисления начинаются с завершающего события и продолжаются последовательно для каждого события сетевого графика вплоть до исходного. Поздний срок свершения завершающего события полагается равным раннему сроку свершения этого события, найденному при прямом проходе. Поздний срок свершения предыдущего события находится простым вычитанием длительности предшествующей работы из позднего срока свершения последующего события.

Если из узла выходят несколько работ, то перед определением позднего срока свершения соответствующего события следует рассмотреть поздние сроки начала для каждой работы, исходящей из этого события. Ясно, что в качестве позднего срока свершения события надо взять поздний срок начала той работы, которая должна начаться первой по времени.

В данном примере:

t_п[8] = 15;

t_п[7] = t_п[8] – t₇₈ = 15 – 2 = 13;

t_п[6] = t_п[7] – t₆₇ = 13 – 3 = 10;

t_п[5] = t_п[7] – t₅₇ = 13 – 1 = 12;

t_п[4] = t_п[7] – t₄₇ = 13 – 4 = 9;

t_п[3] = min(t_п[4] – t₃₄, t_п[5] – t₃₅,t_п[6] – t₃₆) =

= min(9 –3, 12 –2, 10 – 1) = 13;

t_п[2] = min(t_п[3] – t₂₃, t_п[5] – t₂₅) = min(6 –2, 12 –3) = 4;

t_п[1] = t_п[2] – t₁₂ = 4 – 4 = 0;

Полученные значения показаны на сетевом графике (рис.3).

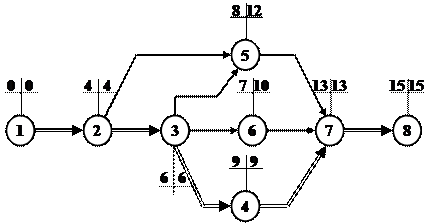
Рис.3. Поздние сроки свершения событий.

Используя результаты вычислений при прямом и обратном проходах, можно определить критический путь. Работа принадлежит критическому пути, если ранние и поздние сроки свершения начального и конечного событий работы совпадают, а между ранними (или поздними) сроками свершения ее конечного и начального событий равна продолжительности этой работы. Для нашего примера критический путь показан двойными линиями.

3. Линейный график работ, построенный в соответствии с описанной ранее процедурой, показан на рис.4.

Линейный график работ идентифицирует работы, отражает логику, указывает резерв. Недостатком линейного графика, отсутствующим у сетевого графика, является его негибкость. Моменты раннего начала и позднего окончания работы должны быть определены до того, как соответствующий отрезок будет нанесен на график. Если проект отстает или опережает расписание, то линейный график работ должен быть перестроен заново из-за жесткой связи между работами.

А	1-2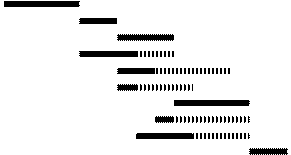
В	2-3
Н	3-4
С	2-5
D	3-5
F	3-6
I	4-7
Е	5-7
G	6-7
J	7-8

Рис.4. Линейный график работ

Дата добавления: 2014-01-11