Проводники в электростатическом поле

Проводником называют вещества, содержащие свободные заряженные частицы, которые могут упорядоченно двигаться под действием электрического поля. Типичным примером проводника является любой металл, где электроны свободно перемещаются между узлами кристаллической решетки. Поместим незаряженный металл в однородное электростатическое поле 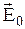. Под влиянием поля свободные электроны проводника начнут перемещаться про­тив поля (рис.1.23). В результате в данном случае левая часть проводника заря­дится отрицательно, а правая, на которой окажется недостаток электронов - поло­жительно. Это явление называется электростатической индукцией. Индуцирован­ные заряды создадут внутри проводника свое поле 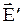, направленное противопо­ложно внешнему 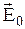. Перераспределение зарядов в проводнике будет происходить до тех пор, пока поле 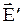не скомпенсирует 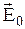. При этом суммарная напряженность поля внутри проводника станет равной нулю и движение зарядов прекратится. Так как внутри проводника , то 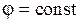. Это означает, что все точки внутри проводника имеют одинаковый потенциал, т.е. проводник является эквипотенциальным те­лом.

На поверхности проводника напряжен­ность поля перпендикулярна к ней, т.е. , где 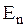- нормальная (т.е. перпендикулярная к поверхности) составля­ющая напряженности. При этом 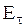- тангенциальная (касательная к поверхности) составляющая напряженности равна нулю, так как в против­ном случае свободные электроны продолжали бы перемещаться на поверхности под действием 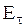, а этого не происходит. Т.е. 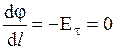, где d l - элемент длины поверхности проводника. Отсюда 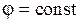, т.е. поверх­ность проводника тоже эквипотенциальна. Таким образом внутри проводника и 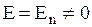на его поверхности, т.е. имеется разрыв непрерывности на поверхно­сти проводни­ка, что объясняется наличием поверхностной плотности заряда s. Введение незаряженного проводника в однородное электростатическое поле искажает его: вблизи проводника оно становится неоднородным.

Если проводник заряжен, то сообщенные ему заряды будут удаляться друг от друга под действием кулоновских сил отталкивания и распределяться только на по­верхности проводника. Внутри проводника не скомпенсированных зарядов не будет. Проведем внутри проводника произвольную замкнутую поверхность S. По теореме Гаусса следует 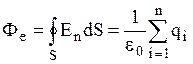. Так как Е внутри проводника нет, то 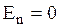и .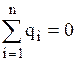

Рис.1.24. К определению на­пряженности поля Е вблизи поверхности заряженного проводника.

Свойство зарядов размещаться только на внешней поверхности проводника ис­пользуется для электростатической защиты (экранирования) тел, измерительных приборов от внешних электростатических полей. Электростатическое экранирова­ние применяется для устранения влияния электричес­ких полей одних электрических цепей на другие. Впервые электростатический экран был сконструиро­ван Фараде­ем (клетка Фарадея). Экраном служила замкнутая про­волочная сетка, внутри которой поме­щался наблюда­тель с приборами, посредством кото­рых и удалось до­казать независимость внутреннего пространства от внешних электростатических полей. Материал, густота и толщина сетки не играют особой роли. На этом прин­ципе основана защита от молнии особенно взрыво­опасных объектов, например, пороховых складов. Крыша и стены таких складов покрываются металлической сеткой, которая должна быть заземлена.

Определим напряженность поля вблизи заряженного проводника. Для этого выделим на его поверхности S малую площадку dS и построим не ней цилиндр с об­разующей l перпендикулярной поверхности и основаниями равными dS (рис.1.24). По­ток напряженности электрического поля через боковую поверхность цилиндра равен нулю, так как параллельна l. Поток через нижнее основание тоже равен нулю, так как внутри проводника поля нет. Таким образом, поток через верхнее осно­вание цилиндра и есть суммарный поток через всю цилиндрическую поверх­ность. Применяя теорему Гаусса, получим , , где s - поверхностная плотность смещенных зарядов. Смещенные индуцированные заряды появляются на поверхности проводника, вследствие их перемещения под дей­ствием электрического поля. Из полученной формулы можно сделать следую­щий вы­вод: напряженность поля вблизи поверхности заряженного проводника опреде­ляется поверхностной плотностью зарядов, находящихся на нем.

Если проводник находится в среде с диэлектрической проницаемостью e, то . Так как 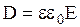, то D = s. Следовательно, электростатическое смещение (или индукция) численно равно поверхностной плотности смещенных зарядов на поверхности проводника. Поэтому вектор и назвали вектором электрического смеще­ния.

Распределение зарядов на поверхности проводника, т.е. величина s, зависит только от его формы. Наибольшая плотность заряда (в силу отталкивания одноименных за­ря­дов) оказывается на наиболее выпуклых местах поверх­нос­ти - на ребрах и остриях. Вблизи этих мест напряжен­ность поля Е максимальна.

Дата добавления: 2014-01-11