Энергия заряженного уединенного проводника, конденсатора. Энергия электростатического поля

Энергия заряженного проводника численно равна работе, которую должны со­вершить внешние силы для его зарядки W=A. При перенесении заряда dq из бесконечности на проводник совершается ра­бота dA против сил электростатического поля (по преодолению кулоновских сил отталки­вания между одноименными зарядами): dA=jdq=Cjdj.

Чтобы зарядить тело от нулевого потенциала до потенциала j, потребуется ра­бота 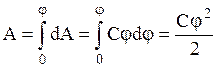. Энергия заряженного проводника равна той работе, которую надо совершить, чтобы зарядить его: .

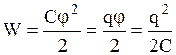Выражение 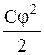принято называть собственной энергией заряженного про­водника.

Увеличение потенциала j проводника при его зарядке сопровождается усиле­нием электростатического поля, возрастает напряженность поля . Естественно предположить, что собственная энергия заряженного проводника есть энергия его электростатического поля. Проверим это предположение на примере однородного поля плоского конденсатора. Повторяя ход вышеприведенного расчета, нетрудно получить энергию заряженного плоского конденсатора ,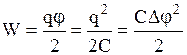

где Dj - разность потенциалов его обкладок. Подставим в эту формулу выражения для емкости плоского конденсатора 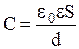и разности потенциалов между обкладками 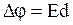. Тогда для энергии получим 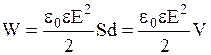, где V=Sd - объем электростатического поля между обкладками конденсатора.

Отсюда следует, что собственная энергия заряженного плоского конденсатора пропорциональна V объему его поля и на­пря­женности . Следовательно, необходимо считать, что электростатическое поле обладает энергией. Объемная плотность энергии электрического поля или энергия единицы объема равна 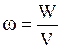, 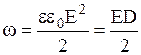. Где же локализована энергия электростатического поля и что является ее но­си­телем - заряды или само поле? Ответ на этот вопрос может дать только опыт. Од­нако электростатика не может ответить на данный вопрос, потому что она изучает посто­янные во времени поля неподвижных зарядов, т.е. в электростатике поля и за­ряды неотделимы друг от друга.

Опыты показали, что переменные во времени электрические поля могут суще­ствовать обособленно, независимо от возбудивших их зарядов. Они распространя­ют­ся в пространстве в виде волн, способных переносить энергию. Отсюда следует, что энергия локализована в поле и носителем электрической энергии является поле.

Дата добавления: 2014-01-11