Тема 5. Ранговая корреляция и возможности ее применения в управленческой и юридической деятельности

До настоящего времени ранговая корреляция не получила широкого распространения при статистической обработке правовой информации. Тем не менее, знание ее возможностей полезно, поскольку речь идет, в частности, об обработке результатов экспертных оценок.

Допустим, что объекты генеральной совокупности обладают двумя качественными признаками. Под качественным подразумевается признак, который невозможно измерить точно, но позволяющий сравнивать объекты между собой и, следовательно, располагать их в порядке возрастания или убывания качества. В дальнейшем будем считать, что объекты располагаются в порядке ухудшения качества. При таком ранжировании первым располагается объект наивысшего качества, вторым – хуже первого, но лучше остальных и т.д.

Пусть выборка объема n содержит независимые объекты, которые обладают двумя качественными признаками А и В. Для оценки степени связи признаков вводят коэффициенты ранговой корреляции Спирмена и Кендалла.

Для практических целей использование ранговой корреляции может быть полезно, например, в случае, когда установление высокой ранговой корреляции между двумя качественными признаками позволяет контролировать только один из них, что может существенно ускорить и удешевить контроль.

Рассмотрим простой случай, когда все объекты имеют различное качество по обоим признакам.

Расположим объекты в порядке ухудшения качества по признаку А. Припишем объекту, стоящему на i -том месте ранг x_i, равный порядковому номеру объекта: x ₁=1, x ₂=2,…, x_n = n.

Далее расположим объекты в порядке убывания качества по признаку В и припишем каждому ранг y_i, индекс i при y будет по прежнему равен порядковому номеру объекта по признаку А. Например запись y ₃=7 означает, что по признаку А объект стоит на третьем месте, а по признаку В – на седьмом.

Получим две последовательности рангов:

по признаку А	x 1	x 2	…	xn
по признаку В	y 1	y 2	…	yn

Допустим, что правее y ₁ имеется R ₁ рангов, больших y ₁; правее y ₂ имеется R ₂ рангов, больших y ₂;…; правее y_{n -1} имеется R_{n -1} рангов, больших y_{n -1}. Введем обозначение R_i (i =1, 2,…, n -1), тогда:

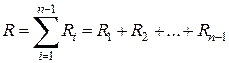
Выборочный коэффициент ранговой корреляции Кендалла:

Возможны следующие крайние случаи по признакам А и В:

1) x_i=y_i. Т.е. ухудшение качества по одному признаку влечет за собой ухудшение качества по другому признаку. Полная прямая зависимость.

2) x ₁=1 и y ₁= n; x ₂=2 и y ₂= n -1… Т.е. ранги по признакам А и В противоположны. Ухудшение качества по одному признаку ведет к улучшению качества по другому признаку. Противоположная зависимость.

Разумеется, чаще встречается промежуточный вариант.

Коэффициент ранговой корреляции Кендалла обладает следующими свойствами:

1) если между качественными признаками имеется полная прямая зависимость, то ;

2) если между качественными признаками имеется обратная зависимость, то ;

3) если между качественными признаками нет ни "полной прямой", ни "противоположной" зависимости, то 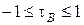. Чем ближе к нулю 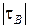, тем зависимость меньше.

Пример 13. Найдем выборочный коэффициент ранговой корреляции Кендалла по следующим рангам объектов выборки n =10:

по А	xi
по В	yi

Решение.

y 1=5, R 1=5	y 2=4, R 2=5	y3=7, R 3=3
y 4=1, R 4=6	y 5=2, R 5=5	y6=8, R 6=2
y 7=10, R 7=0	y 8=3, R 8=2	y9=6, R 9=1

Сумма рангов: R =5+5+3+6+5+2+0+2+1=29.

Искомый коэффициент:

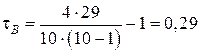
Правило: Чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Кендалла 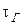при конкурирующей гипотезе Н ₁ () необходимо вычислить критическую точку:

,

где z_кр – критическая точка по таблице функции Лапласа .

Если 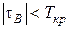– нет оснований отвергать нулевую гипотезу. Ранговая связь между качественными признаками незначимая.

Если – нулевую гипотезу следует отвергнуть. Между качественными признаками существует значимая ранговая корреляционная связь.

Пример 14. По данным примера 13 при уровне значимости 0,1 проверить, является ли ранговая корреляционная связь при значимой.

Решение. Найдем критическую точку z_кр:

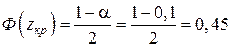
По таблице можно найти z_кр =1,65.

Критическая точка:

Т.к. 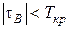нет оснований отвергать нулевую гипотезу – ранговая корреляционная связь между признаками незначимая.

Наряду с коэффициентом ранговой корреляции Кендалла применяется выборочный коэффициент ранговой корреляции Спирмена. Он определяется следующим образом:

,

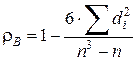где .

Пример 15. По данным примера 13 вычислим выборочный коэффициент ранговой корреляции Спирмена.

Решение.

d 1=-4	d 2=-2	d 3=-4	d 4=3	d 5=3
d 6=-2	d 7=-3	d 8=5	d 9=3	d 10=1

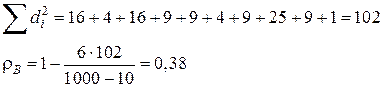
Выборочный коэффициент ранговой корреляции Спирмена обладает теми же свойствами, что и выборочный коэффициент ранговой корреляции Кендалла.

Правило: Чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена 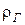при конкурирующей гипотезе Н ₁ () необходимо вычислить критическую точку:

,

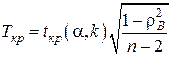где – критическая точка, которую находят по таблице критических точек распределения Стьюдента по уровню значимости α и числу степеней свободы k=n -2.

Если 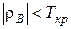– нет оснований отвергать нулевую гипотезу. Ранговая связь между качественными признаками незначимая.

Если – нулевую гипотезу следует отвергнуть. Между качественными признаками существует значимая ранговая корреляционная связь.

Пример 16. По данным примера 13 при уровне значимости 0,1 проверить, является ли ранговая корреляционная связь при значимой.

Решение.

Т.к. 0,38<0,61 нет оснований отвергать нулевую гипотезу, ранговая корреляционная связь между признаками незначимая.

Пример 17. По решению начальника УВД по N-ской области группа экспертов провела комплексную оценку деятельности ряда районных отделов внутренних дел. Комплексная оценка должна содержать информацию о различных показателях работы – раскрываемости, кадровой ситуации и т.д. Удельный вес каждого показателя внутри комплексной оценки обосновать затруднительно, поэтому оценка должна быть сделана ранжированной в порядке ухудшения комплексного показателя.

Эксперты предложили два подхода к формированию комплексного показателя, поэтому каждый райотдел получил две оценки.

Необходимо оценить корреляционную связь между предложенными показателями и сделать вывод – является ли эта связь значимой, т.е. можно контролировать только один из предложенных комплексных показателей. Уровень значимости принять равным 0,05.

Исходные данные:

Таблица 6.1

Район	Комплексный показатель 1 (xi)	Комплексный показатель 2 (yi)
Советский
Зареченский
Привокзальный
Центральный
Пролетарский
Белевский
Арсеньевский
Алексинский

Решение. Рассмотрим нулевую гипотезу – связь между комплексными показателями незначимая.

Преобразуем исходную таблицу к следующему виду и найдем разность комплексных показателей:

xi
yi
di	-2		-3				-1

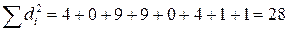
Выборочный коэффициент ранговой корреляции Спирмена:

.

Найдем критическую точку при уровне значимости α=0,05:

Поскольку 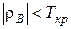– нет оснований отвергать нулевую гипотезу. Ранговая связь между качественными признаками незначимая, нельзя контролировать только один из предложенных комплексных показателей.

Дата добавления: 2014-01-11